Embeddings sind zum Eckpfeiler verschiedener KI- und Natural Language Processing-Anwendungen geworden und bieten eine Möglichkeit, die Bedeutung von Texten als hochdimensionale Vektoren darzustellen. Mit der zunehmenden Größe der Modelle und der wachsenden Datenmenge, die KI-Modelle verarbeiten, sind jedoch die Rechen- und Speicheranforderungen für traditionelle Embeddings gestiegen. Binäre Embeddings wurden als kompakte, effiziente Alternative eingeführt, die hohe Leistung bei drastisch reduzierten Ressourcenanforderungen beibehält.
Binäre Embeddings sind eine Möglichkeit, diese Ressourcenanforderungen zu reduzieren, indem die Größe der Embedding-Vektoren um bis zu 96% verringert wird (96,875% im Fall von Jina Embeddings). Benutzer können die Leistungsfähigkeit kompakter binärer Embeddings in ihren KI-Anwendungen mit minimalem Genauigkeitsverlust nutzen.
tagWas sind Binäre Embeddings?
Binäre Embeddings sind eine spezielle Form der Datenrepräsentation, bei der traditionelle hochdimensionale Gleitkomma-Vektoren in binäre Vektoren umgewandelt werden. Dies komprimiert nicht nur die Embeddings, sondern behält auch fast die gesamte Integrität und Nützlichkeit der Vektoren bei. Das Wesentliche dieser Technik liegt in ihrer Fähigkeit, die Semantik und relationalen Abstände zwischen den Datenpunkten auch nach der Konvertierung beizubehalten.
Die Magie hinter binären Embeddings ist die Quantisierung, eine Methode, die hochpräzise Zahlen in Zahlen mit niedrigerer Präzision umwandelt. In der KI-Modellierung bedeutet dies oft, die 32-Bit-Gleitkommazahlen in Embeddings in Darstellungen mit weniger Bits, wie 8-Bit-Ganzzahlen, umzuwandeln.

Binäre Embeddings treiben dies auf die Spitze, indem sie jeden Wert auf 0 oder 1 reduzieren. Die Umwandlung von 32-Bit-Gleitkommazahlen in binäre Ziffern reduziert die Größe der Embedding-Vektoren um das 32-fache, eine Reduktion von 96,875%. Vektoroperationen auf den resultierenden Embeddings sind dadurch viel schneller. Die Nutzung von Hardware-Beschleunigungen, die auf einigen Mikrochips verfügbar sind, kann die Geschwindigkeit von Vektorvergleichen bei binarisierten Vektoren um weit mehr als das 32-fache erhöhen.
Bei diesem Prozess gehen zwangsläufig einige Informationen verloren, aber dieser Verlust wird minimiert, wenn das Modell sehr leistungsfähig ist. Wenn die nicht-quantisierten Embeddings verschiedener Dinge maximal unterschiedlich sind, dann ist es wahrscheinlicher, dass die Binarisierung diesen Unterschied gut bewahrt. Andernfalls kann es schwierig sein, die Embeddings korrekt zu interpretieren.
Jina Embeddings Modelle sind darauf trainiert, genau in dieser Hinsicht sehr robust zu sein, was sie für die Binarisierung besonders geeignet macht.
Solche kompakten Embeddings ermöglichen neue KI-Anwendungen, insbesondere in ressourcenbeschränkten Kontexten wie mobilen und zeitkritischen Anwendungen.
Diese Kosten- und Rechenzeitvorteile kommen mit relativ geringen Leistungseinbußen, wie die folgende Grafik zeigt.

Für jina-embeddings-v2-base-en reduziert die binäre Quantisierung die Abrufgenauigkeit von 47,13% auf 42,05%, ein Verlust von etwa 10%. Für jina-embeddings-v2-base-de beträgt dieser Verlust nur 4%, von 44,39% auf 42,65%.
Jina Embeddings Modelle schneiden bei der Erzeugung binärer Vektoren so gut ab, weil sie darauf trainiert sind, eine gleichmäßigere Verteilung von Embeddings zu erzeugen. Dies bedeutet, dass zwei verschiedene Embeddings wahrscheinlich in mehr Dimensionen weiter voneinander entfernt sind als Embeddings aus anderen Modellen. Diese Eigenschaft stellt sicher, dass diese Abstände besser durch ihre binären Formen repräsentiert werden.
tagWie funktionieren Binäre Embeddings?
Um zu verstehen, wie das funktioniert, betrachten wir drei Embeddings: A, B und C. Diese drei sind alle vollständige Gleitkomma-Vektoren, keine binarisierten. Nehmen wir an, der Abstand von A zu B ist größer als der Abstand von B zu C. Bei Embeddings verwenden wir typischerweise die Kosinus-Distanz, also:
Wenn wir A, B und C binarisieren, können wir den Abstand effizienter mit der Hamming-Distanz messen.
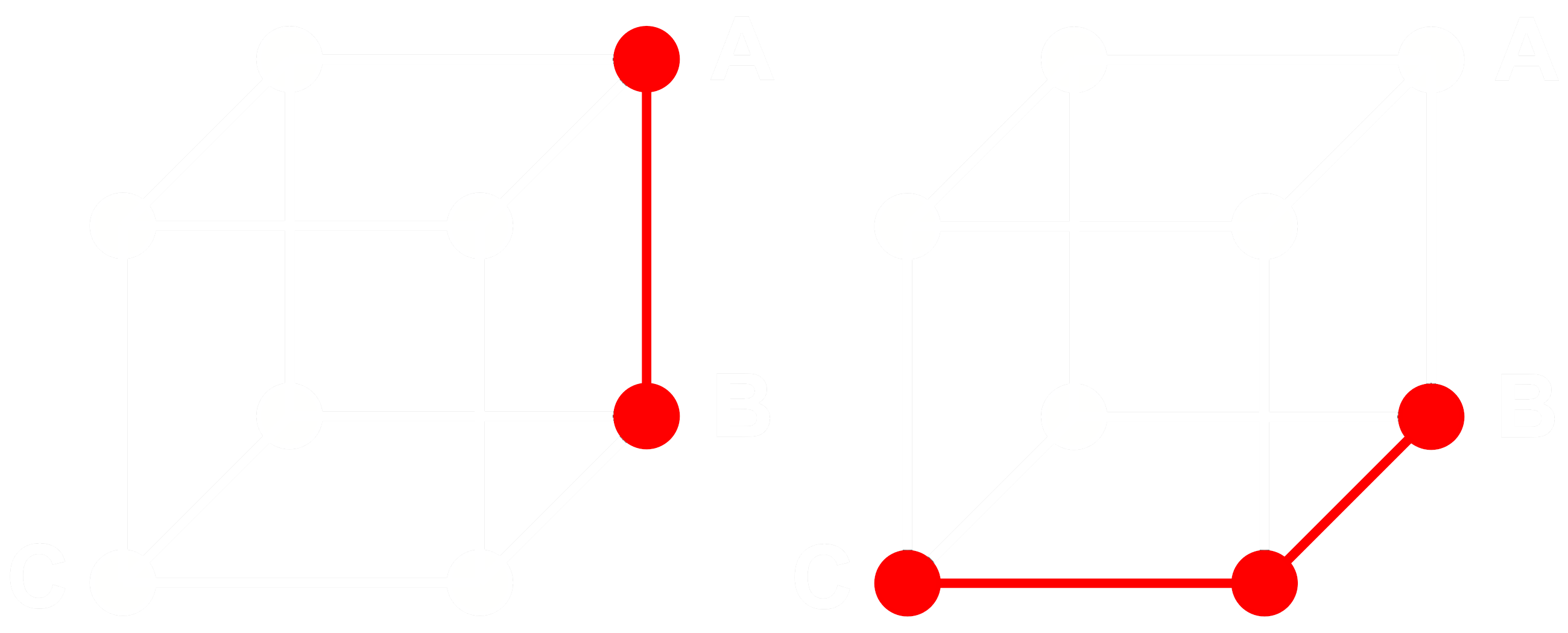
Nennen wir Abin, Bbin und Cbin die binarisierten Versionen von A, B und C.
Bei binären Vektoren gilt: Wenn die Kosinus-Distanz zwischen Abin und Bbin größer ist als zwischen Bbin und Cbin, dann ist die Hamming-Distanz zwischen Abin und Bbin größer oder gleich der Hamming-Distanz zwischen Bbin und Cbin.
Also wenn:
dann gilt für Hamming-Distanzen:
Idealerweise wollen wir bei der Binarisierung von Embeddings, dass die gleichen Beziehungen wie bei den vollständigen Embeddings auch für die binären Embeddings gelten. Das bedeutet, wenn ein Abstand größer als ein anderer für Gleitkomma-Kosinus ist, sollte er auch für die Hamming-Distanz zwischen ihren binarisierten Äquivalenten größer sein:
Wir können dies nicht für alle Tripel von Embeddings garantieren, aber wir können es für fast alle erreichen.
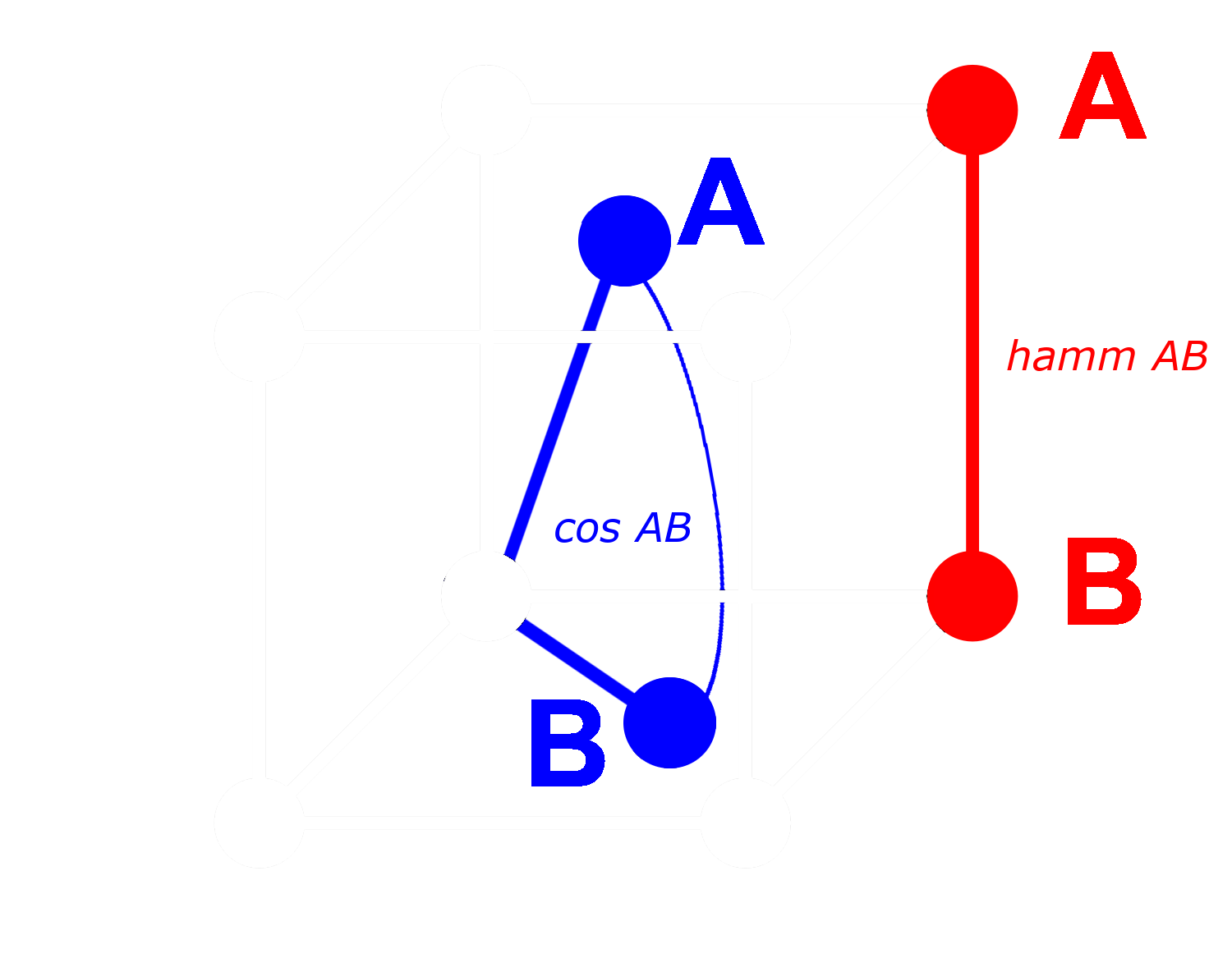
Bei einem binären Vektor können wir jede Dimension entweder als vorhanden (eine Eins) oder nicht vorhanden (eine Null) behandeln. Je weiter zwei Vektoren in nicht-binärer Form voneinander entfernt sind, desto höher ist die Wahrscheinlichkeit, dass in einer bestimmten Dimension einer einen positiven Wert und der andere einen negativen Wert hat. Das bedeutet, dass es in binärer Form höchstwahrscheinlich mehr Dimensionen gibt, wo einer eine Null und der andere eine Eins hat. Dies macht sie nach Hamming-Distanz weiter voneinander entfernt.
Das Gegenteil gilt für Vektoren, die näher beieinander liegen: Je näher die nicht-binären Vektoren sind, desto höher ist die Wahrscheinlichkeit, dass in einer Dimension beide Nullen oder beide Einsen haben. Dies macht sie nach Hamming-Distanz näher beieinander.
Jina Embeddings Modelle sind für die Binarisierung so gut geeignet, weil wir sie mit Negative Mining und anderen Fine-Tuning-Praktiken trainieren, um besonders den Abstand zwischen unähnlichen Dingen zu vergrößern und den Abstand zwischen ähnlichen zu verringern. Dies macht die Embeddings robuster, empfindlicher für Ähnlichkeiten und Unterschiede und sorgt dafür, dass die Hamming-Distanz zwischen binären Embeddings proportionaler zur Kosinus-Distanz zwischen nicht-binären ist.
tagWie viel kann ich mit Jina AIs Binären Embeddings sparen?
Die Nutzung von Jina AIs binären Embedding-Modellen senkt nicht nur die Latenz in zeitkritischen Anwendungen, sondern bringt auch erhebliche Kostenvorteile, wie die folgende Tabelle zeigt:
| Model | Speicher pro 250 Millionen Embeddings |
Retrieval Benchmark Durchschnitt |
Geschätzter Preis auf AWS ($3,8 pro GB/Monat mit x2gb Instanzen) |
|---|---|---|---|
| 32-bit Gleitkomma-Embeddings | 715 GB | 47,13 | $35.021 |
| Binäre Embeddings | 22,3 GB | 42,05 | $1.095 |
Diese Einsparung von über 95 % geht mit einer nur etwa 10%igen Reduzierung der Abrufgenauigkeit einher.
Diese Einsparungen sind sogar noch größer als bei der Verwendung binärisierter Vektoren von OpenAIs Ada 2 Modell oder Coheres Embed v3, die beide Ausgabe-Embeddings von 1024 oder mehr Dimensionen erzeugen. Jina AIs Embeddings haben nur 768 Dimensionen und liefern dennoch vergleichbare Leistung wie andere Modelle, wodurch sie selbst vor der Quantisierung bei gleicher Genauigkeit kleiner sind.
Diese Einsparungen sind auch umweltfreundlich, da sie weniger seltene Materialien und weniger Energie verbrauchen.
tagErste Schritte
Um binäre Embeddings über die Jina Embeddings API zu erhalten, fügen Sie einfach den Parameter encoding_type zu Ihrem API-Aufruf hinzu, mit dem Wert binary für das als vorzeichenbehaftete Ganzzahlen kodierte binäre Embedding oder ubinary für vorzeichenlose Ganzzahlen.
tagDirekter Zugriff auf die Jina Embedding API
Mit curl:
curl https://api.jina.ai/v1/embeddings \
-H "Content-Type: application/json" \
-H "Authorization: Bearer <YOUR API KEY>" \
-d '{
"input": ["Your text string goes here", "You can send multiple texts"],
"model": "jina-embeddings-v2-base-en",
"encoding_type": "binary"
}'
Oder über die Python requests API:
import requests
headers = {
"Content-Type": "application/json",
"Authorization": "Bearer <YOUR API KEY>"
}
data = {
"input": ["Your text string goes here", "You can send multiple texts"],
"model": "jina-embeddings-v2-base-en",
"encoding_type": "binary",
}
response = requests.post(
"https://api.jina.ai/v1/embeddings",
headers=headers,
json=data,
)
Mit dem obigen Python request erhalten Sie die folgende Antwort durch Überprüfung von response.json():
{
"model": "jina-embeddings-v2-base-en",
"object": "list",
"usage": {
"total_tokens": 14,
"prompt_tokens": 14
},
"data": [
{
"object": "embedding",
"index": 0,
"embedding": [
-0.14528547,
-1.0152762,
...
]
},
{
"object": "embedding",
"index": 1,
"embedding": [
-0.109809875,
-0.76077706,
...
]
}
]
}
Dies sind zwei binäre Embedding-Vektoren, die als 96 8-Bit vorzeichenbehaftete Ganzzahlen gespeichert sind. Um sie in 768 Nullen und Einsen zu entpacken, müssen Sie die numpy Bibliothek verwenden:
import numpy as np
# assign the first vector to embedding0
embedding0 = response.json()['data'][0]['embedding']
# convert embedding0 to a numpy array of unsigned 8-bit ints
uint8_embedding = np.array(embedding0).astype(numpy.uint8)
# unpack to binary
np.unpackbits(uint8_embedding)
Das Ergebnis ist ein 768-dimensionaler Vektor, der nur aus Nullen und Einsen besteht:
array([0, 0, 1, 1, 0, 1, 1, 0, 1, 1, 0, 0, 0, 1, 0, 1, 1, 1, 1, 1, 0, 0,
0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 1, 1, 0, 0, 0, 1, 1, 1, 0, 1, 0, 1,
0, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 1, 1, 0, 0, 0, 0, 1, 0, 1, 1, 1,
0, 0, 0, 0, 1, 1, 1, 0, 0, 1, 0, 0, 0, 0, 1, 1, 1, 1, 0, 1, 0, 1,
1, 1, 0, 1, 1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 0, 0, 0,
0, 0, 1, 0, 0, 0, 1, 0, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1, 0, 0, 1, 0,
1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 1,
1, 0, 1, 0, 1, 1, 0, 0, 0, 1, 0, 1, 1, 1, 0, 0, 1, 1, 0, 0, 0, 1,
1, 1, 0, 1, 0, 1, 1, 1, 1, 0, 1, 0, 0, 1, 0, 0, 1, 0, 1, 0, 1, 1,
0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 1, 1, 0, 1, 0, 0, 0, 1, 1, 1,
1, 0, 0, 1, 0, 0, 0, 1, 0, 1, 0, 0, 1, 0, 1, 0, 1, 0, 0, 1, 0, 0,
0, 0, 0, 0, 1, 0, 0, 0, 1, 1, 1, 0, 1, 1, 0, 1, 1, 0, 1, 0, 0, 0,
1, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1, 1, 0, 1, 1, 0, 0, 0, 1, 0, 0, 1,
0, 0, 0, 0, 0, 1, 1, 0, 0, 1, 1, 1, 1, 0, 1, 0, 1, 0, 1, 1, 1, 1,
1, 0, 1, 0, 0, 0, 1, 0, 0, 1, 0, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 0,
0, 0, 0, 0, 1, 0, 1, 1, 1, 0, 1, 1, 1, 1, 0, 0, 0, 0, 0, 1, 1, 1,
1, 1, 1, 1, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 1, 0, 1, 0, 1,
1, 0, 1, 1, 1, 0, 0, 1, 0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 0, 0, 1, 1,
0, 0, 0, 1, 1, 1, 1, 1, 0, 1, 1, 0, 1, 0, 0, 0, 1, 1, 0, 1, 1, 0,
1, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 1, 1, 1, 0, 1, 1, 1, 0,
0, 0, 0, 0, 0, 1, 1, 1, 1, 0, 1, 0, 1, 1, 0, 1, 0, 1, 1, 1, 0, 0,
0, 0, 1, 1, 1, 0, 1, 0, 1, 0, 0, 1, 0, 1, 0, 0, 0, 1, 1, 1, 0, 1,
0, 1, 1, 1, 0, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 0, 0, 1, 0,
0, 1, 1, 1, 0, 1, 1, 0, 0, 1, 1, 0, 1, 1, 0, 1, 1, 1, 0, 1, 1, 0,
1, 1, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 1, 1, 1, 0, 1, 1, 0,
0, 1, 0, 0, 1, 1, 0, 1, 0, 0, 1, 0, 0, 1, 0, 1, 0, 1, 1, 1, 0, 0,
0, 0, 1, 1, 0, 1, 0, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 0, 1,
1, 0, 1, 1, 0, 1, 1, 0, 1, 0, 0, 1, 0, 0, 0, 1, 0, 1, 0, 1, 1, 0,
1, 1, 1, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1, 0, 0, 1, 0, 1, 1, 0, 0,
1, 0, 1, 1, 1, 1, 1, 1, 1, 0, 1, 0, 0, 0, 1, 0, 0, 1, 1, 1, 0, 1,
1, 1, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 1, 1, 0, 1, 1, 0, 0, 1, 1, 0,
1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 1, 0, 0, 1, 1, 0, 1,
1, 1, 1, 0, 0, 1, 1, 1, 0, 1, 0, 0, 1, 1, 0, 1, 1, 1, 1, 1, 1, 0,
1, 1, 1, 0, 0, 1, 1, 0, 0, 1, 0, 0, 1, 1, 0, 0, 0, 1, 0, 1, 1, 1,
0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 0, 1, 0, 0],
dtype=uint8)
tagVerwendung der binären Quantisierung in Qdrant
Sie können auch die Qdrant-Integrationsbibliothek verwenden, um binäre Embeddings direkt in Ihrem Qdrant Vector Store zu speichern. Da Qdrant BinaryQuantization intern implementiert hat, können Sie es als voreingestellte Konfiguration für die gesamte Vektorsammlung verwenden, wodurch binäre Vektoren ohne weitere Änderungen an Ihrem Code abgerufen und gespeichert werden können.
Sehen Sie sich das Beispiel im folgenden Code an:
import qdrant_client
import requests
from qdrant_client.models import Distance, VectorParams, Batch, BinaryQuantization, BinaryQuantizationConfig
# Stellen Sie den Jina API-Schlüssel bereit und wählen Sie eines der verfügbaren Modelle.
# Sie können hier einen kostenlosen Testschlüssel erhalten: https://jina.ai/embeddings/
JINA_API_KEY = "jina_xxx"
MODEL = "jina-embeddings-v2-base-en" # oder "jina-embeddings-v2-base-en"
EMBEDDING_SIZE = 768 # 512 für kleine Variante
# Embeddings von der API abrufen
url = "https://api.jina.ai/v1/embeddings"
headers = {
"Content-Type": "application/json",
"Authorization": f"Bearer {JINA_API_KEY}",
}
text_to_encode = ["Your text string goes here", "You can send multiple texts"]
data = {
"input": text_to_encode,
"model": MODEL,
}
response = requests.post(url, headers=headers, json=data)
embeddings = [d["embedding"] for d in response.json()["data"]]
# Die Embeddings in Qdrant indexieren
client = qdrant_client.QdrantClient(":memory:")
client.create_collection(
collection_name="MyCollection",
vectors_config=VectorParams(size=EMBEDDING_SIZE, distance=Distance.DOT, on_disk=True),
quantization_config=BinaryQuantization(binary=BinaryQuantizationConfig(always_ram=True)),
)
client.upload_collection(
collection_name="MyCollection",
ids=list(range(len(embeddings))),
vectors=embeddings,
payload=[
{"text": x} for x in text_to_encode
],
)Für die Suchkonfiguration sollten Sie die Parameter oversampling und rescore verwenden:
from qdrant_client.models import SearchParams, QuantizationSearchParams
results = client.search(
collection_name="MyCollection",
query_vector=embeddings[0],
search_params=SearchParams(
quantization=QuantizationSearchParams(
ignore=False,
rescore=True,
oversampling=2.0,
)
)
)tagVerwendung von LlamaIndex
Um Jina Binary Embeddings mit LlamaIndex zu verwenden, setzen Sie den Parameter encoding_queries auf binary bei der Instanziierung des JinaEmbedding Objekts:
from llama_index.embeddings.jinaai import JinaEmbedding
# Sie können einen kostenlosen Testschlüssel von https://jina.ai/embeddings/ erhalten
JINA_API_KEY = "<YOUR API KEY>"
jina_embedding_model = JinaEmbedding(
api_key=jina_ai_api_key,
model="jina-embeddings-v2-base-en",
encoding_queries='binary',
encoding_documents='float'
)
jina_embedding_model.get_query_embedding('Query text here')
jina_embedding_model.get_text_embedding_batch(['X', 'Y', 'Z'])
tagAndere Vektordatenbanken mit Unterstützung für binäre Embeddings
Die folgenden Vektordatenbanken bieten native Unterstützung für binäre Vektoren:
tagBeispiel
Um binäre Embeddings in Aktion zu zeigen, haben wir eine Auswahl von Abstracts von arXiv.org genommen und sowohl 32-Bit-Fließkomma- als auch binäre Vektoren mit jina-embeddings-v2-base-en erstellt. Dann haben wir sie mit den Embeddings für eine Beispielabfrage verglichen: "3D segmentation."
Wie Sie aus der untenstehenden Tabelle ersehen können, sind die Top-3-Antworten identisch und vier der Top-5 stimmen überein. Die Verwendung binärer Vektoren liefert nahezu identische Top-Treffer.
| Binary | 32-bit Float | |||
|---|---|---|---|---|
| Rang | Hamming Dist. |
Übereinstimmender Text | Kosinus | Übereinstimmender Text |
| 1 | 0.1862 | SEGMENT3D: A Web-based Application for Collaboration... |
0.2340 | SEGMENT3D: A Web-based Application for Collaboration... |
| 2 | 0.2148 | Segmentation-by-Detection: A Cascade Network for... |
0.2857 | Segmentation-by-Detection: A Cascade Network for... |
| 3 | 0.2174 | Vox2Vox: 3D-GAN for Brain Tumour Segmentation... |
0.2973 | Vox2Vox: 3D-GAN for Brain Tumour Segmentation... |
| 4 | 0.2318 | DiNTS: Differentiable Neural Network Topology Search... |
0.2983 | Anisotropic Mesh Adaptation for Image Segmentation... |
| 5 | 0.2331 | Data-Driven Segmentation of Post-mortem Iris Image... |
0.3019 | DiNTS: Differentiable Neural Network Topology... |