Los embeddings se han convertido en la piedra angular de una variedad de aplicaciones de IA y procesamiento de lenguaje natural, ofreciendo una forma de representar los significados de los textos como vectores multidimensionales. Sin embargo, entre el creciente tamaño de los modelos y las cantidades cada vez mayores de datos que procesan los modelos de IA, las demandas computacionales y de almacenamiento para los embeddings tradicionales han aumentado. Los embeddings binarios se han introducido como una alternativa compacta y eficiente que mantiene un alto rendimiento mientras reduce drásticamente los requisitos de recursos.
Los embeddings binarios son una forma de mitigar estos requisitos de recursos reduciendo el tamaño de los vectores de embedding hasta en un 96% (96.875% en el caso de Jina Embeddings). Los usuarios pueden aprovechar el poder de los embeddings binarios compactos en sus aplicaciones de IA con una pérdida mínima de precisión.
tag¿Qué Son los Embeddings Binarios?
Los embeddings binarios son una forma especializada de representación de datos donde los vectores tradicionales de punto flotante de alta dimensión se transforman en vectores binarios. Esto no solo comprime los embeddings sino que también retiene casi toda la integridad y utilidad de los vectores. La esencia de esta técnica radica en su capacidad para mantener la semántica y las distancias relacionales entre los puntos de datos incluso después de la conversión.
La magia detrás de los embeddings binarios es la cuantización, un método que convierte números de alta precisión en números de menor precisión. En el modelado de IA, esto a menudo significa convertir los números de punto flotante de 32 bits en representaciones con menos bits, como enteros de 8 bits.

Los embeddings binarios llevan esto a su extremo último, reduciendo cada valor a 0 o 1. Transformar números de punto flotante de 32 bits a dígitos binarios reduce el tamaño de los vectores de embedding 32 veces, una reducción del 96.875%. Las operaciones vectoriales en los embeddings resultantes son mucho más rápidas como resultado. El uso de aceleraciones por hardware disponibles en algunos microchips puede aumentar la velocidad de las comparaciones vectoriales mucho más de 32 veces cuando los vectores están binarizados.
Inevitablemente se pierde algo de información durante este proceso, pero esta pérdida se minimiza cuando el modelo es muy eficiente. Si los embeddings no cuantizados de diferentes cosas son máximamente diferentes, entonces la binarización tiene más probabilidades de preservar bien esa diferencia. De lo contrario, puede ser difícil interpretar los embeddings correctamente.
Los modelos de Jina Embeddings están entrenados para ser muy robustos exactamente de esa manera, haciéndolos muy adecuados para la binarización.
Tales embeddings compactos hacen posibles nuevas aplicaciones de IA, particularmente en contextos con recursos limitados como usos móviles y sensibles al tiempo.
Estos beneficios en costos y tiempo de cómputo vienen con un costo de rendimiento relativamente pequeño, como muestra el gráfico a continuación.

Para jina-embeddings-v2-base-en, la cuantización binaria reduce la precisión de recuperación del 47.13% al 42.05%, una pérdida de aproximadamente 10%. Para jina-embeddings-v2-base-de, esta pérdida es solo del 4%, del 44.39% al 42.65%.
Los modelos de Jina Embeddings funcionan tan bien al producir vectores binarios porque están entrenados para crear una distribución más uniforme de embeddings. Esto significa que dos embeddings diferentes probablemente estarán más alejados entre sí en más dimensiones que los embeddings de otros modelos. Esta propiedad asegura que esas distancias estén mejor representadas por sus formas binarias.
tag¿Cómo Funcionan los Embeddings Binarios?
Para ver cómo funciona esto, consideremos tres embeddings: A, B y C. Estos tres son vectores completos de punto flotante, no binarizados. Ahora, digamos que la distancia de A a B es mayor que la distancia de B a C. Con embeddings, típicamente usamos la distancia coseno, entonces:
Si binarizamos A, B y C, podemos medir la distancia más eficientemente con la distancia de Hamming.
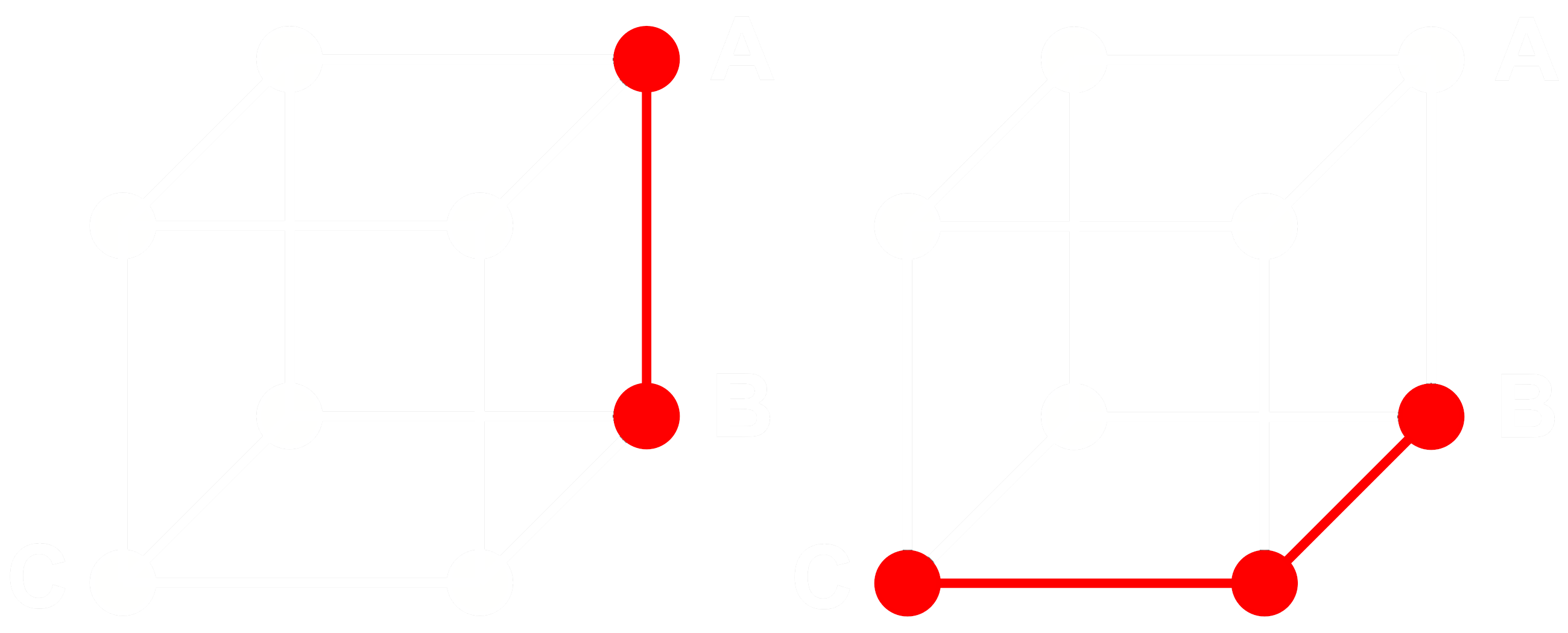
Llamemos Abin, Bbin y Cbin a las versiones binarizadas de A, B y C.
Para vectores binarios, si la distancia coseno entre Abin y Bbin es mayor que entre Bbin y Cbin, entonces la distancia de Hamming entre Abin y Bbin es mayor o igual que la distancia de Hamming entre Bbin y Cbin.
Entonces si:
entonces para distancias de Hamming:
Idealmente, cuando binarizamos embeddings, queremos que las mismas relaciones con embeddings completos se mantengan para los embeddings binarios como para los completos. Esto significa que si una distancia es mayor que otra para el coseno de punto flotante, debería ser mayor para la distancia de Hamming entre sus equivalentes binarizados:
No podemos hacer que esto sea verdadero para todos los tripletes de embeddings, pero podemos hacerlo verdadero para casi todos ellos.
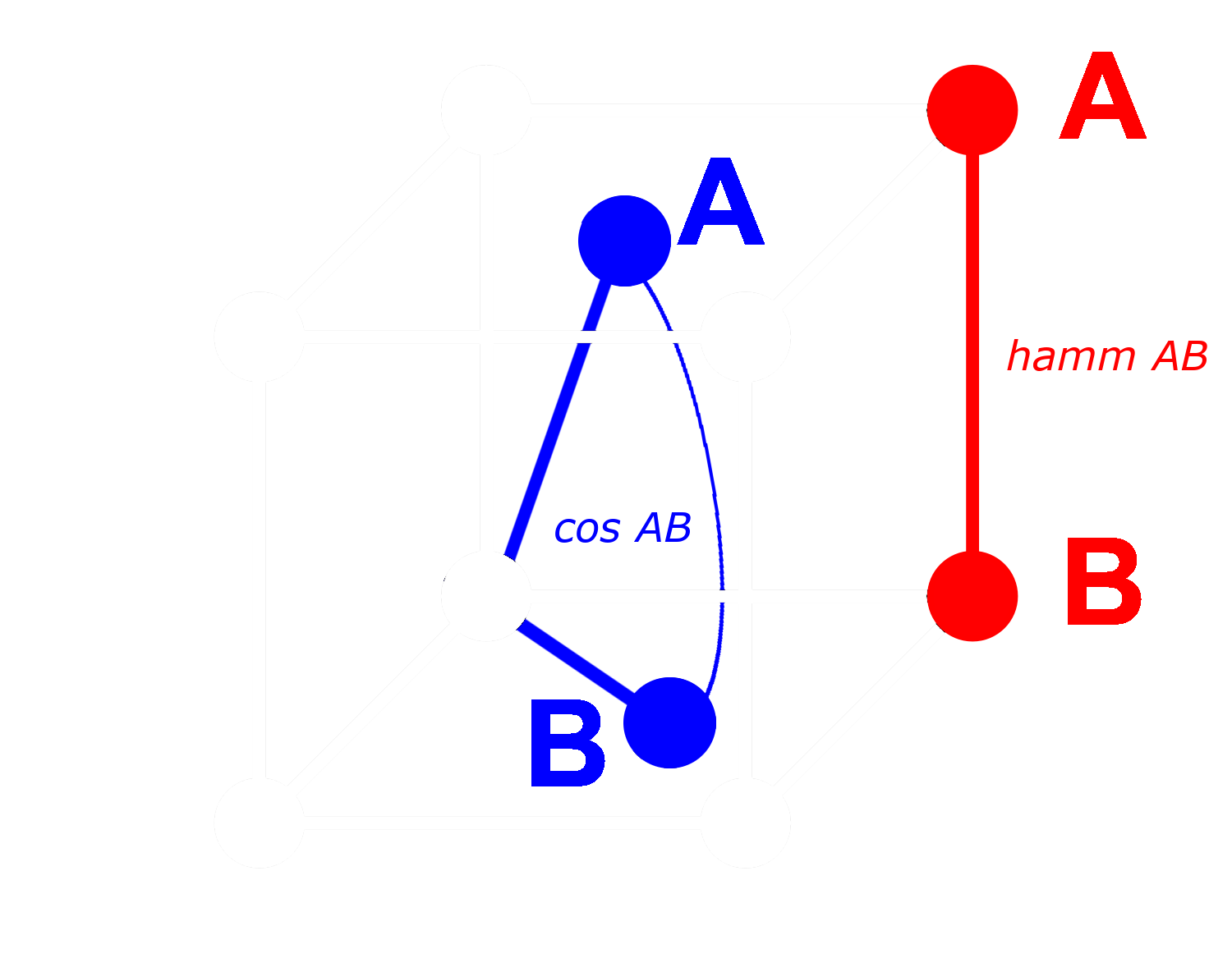
Con un vector binario, podemos tratar cada dimensión como presente (un uno) o ausente (un cero). Cuanto más distantes estén dos vectores entre sí en forma no binaria, mayor será la probabilidad de que en cualquier dimensión, uno tenga un valor positivo y el otro un valor negativo. Esto significa que en forma binaria, probablemente habrá más dimensiones donde uno tenga un cero y el otro un uno. Esto los hace más distantes por distancia de Hamming.
Lo opuesto se aplica a vectores que están más cerca entre sí: Cuanto más cerca estén los vectores no binarios, mayor será la probabilidad de que en cualquier dimensión ambos tengan ceros o ambos tengan unos. Esto los hace más cercanos por distancia de Hamming.
Los modelos de Jina Embeddings son tan adecuados para la binarización porque los entrenamos usando minería negativa y otras prácticas de ajuste fino para aumentar especialmente la distancia entre cosas diferentes y reducir la distancia entre las similares. Esto hace que los embeddings sean más robustos, más sensibles a las similitudes y diferencias, y hace que la distancia de Hamming entre embeddings binarios sea más proporcional a la distancia coseno entre los no binarios.
tag¿Cuánto Puedo Ahorrar con los Embeddings Binarios de Jina AI?
Adoptar los modelos de embedding binario de Jina AI no solo reduce la latencia en aplicaciones sensibles al tiempo, sino que también produce beneficios considerables en costos, como se muestra en la tabla siguiente:
| Modelo | Memoria por 250 millones de embeddings |
Promedio de benchmark de recuperación |
Precio estimado en AWS ($3.8 por GB/mes con instancias x2gb) |
|---|---|---|---|
| Embeddings de punto flotante de 32 bits | 715 GB | 47.13 | $35,021 |
| Embeddings binarios | 22.3 GB | 42.05 | $1,095 |
Este ahorro de más del 95% viene acompañado de solo ~10% de reducción en la precisión de recuperación.
Estos ahorros son incluso mayores que usando vectores binarizados de el modelo Ada 2 de OpenAI o Embed v3 de Cohere, ambos producen embeddings de salida de 1024 dimensiones o más. Los embeddings de Jina AI tienen solo 768 dimensiones y aun así tienen un rendimiento comparable a otros modelos, haciéndolos más pequeños incluso antes de la cuantización para la misma precisión.
Estos ahorros también son ambientales, usando menos materiales raros y menos energía.
tagEmpezar
Para obtener embeddings binarios usando la API de Jina Embeddings, solo agregue el parámetro encoding_type a su llamada API, con el valor binary para obtener el embedding binarizado codificado como enteros con signo, o ubinary para enteros sin signo.
tagAcceder Directamente a la API de Jina Embedding
Usando curl:
curl https://api.jina.ai/v1/embeddings \
-H "Content-Type: application/json" \
-H "Authorization: Bearer <YOUR API KEY>" \
-d '{
"input": ["Your text string goes here", "You can send multiple texts"],
"model": "jina-embeddings-v2-base-en",
"encoding_type": "binary"
}'
O mediante la API de Python requests:
import requests
headers = {
"Content-Type": "application/json",
"Authorization": "Bearer <YOUR API KEY>"
}
data = {
"input": ["Your text string goes here", "You can send multiple texts"],
"model": "jina-embeddings-v2-base-en",
"encoding_type": "binary",
}
response = requests.post(
"https://api.jina.ai/v1/embeddings",
headers=headers,
json=data,
)
Con la request de Python anterior, obtendrá la siguiente respuesta al inspeccionar response.json():
{
"model": "jina-embeddings-v2-base-en",
"object": "list",
"usage": {
"total_tokens": 14,
"prompt_tokens": 14
},
"data": [
{
"object": "embedding",
"index": 0,
"embedding": [
-0.14528547,
-1.0152762,
...
]
},
{
"object": "embedding",
"index": 1,
"embedding": [
-0.109809875,
-0.76077706,
...
]
}
]
}
Estos son dos vectores de embedding binarios almacenados como 96 enteros de 8 bits con signo. Para desempaquetarlos a 768 0's y 1's, necesita usar la biblioteca numpy:
import numpy as np
# assign the first vector to embedding0
embedding0 = response.json()['data'][0]['embedding']
# convert embedding0 to a numpy array of unsigned 8-bit ints
uint8_embedding = np.array(embedding0).astype(numpy.uint8)
# unpack to binary
np.unpackbits(uint8_embedding)
El resultado es un vector de 768 dimensiones con solo 0's y 1's:
array([0, 0, 1, 1, 0, 1, 1, 0, 1, 1, 0, 0, 0, 1, 0, 1, 1, 1, 1, 1, 0, 0,
0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 1, 1, 0, 0, 0, 1, 1, 1, 0, 1, 0, 1,
0, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 1, 1, 0, 0, 0, 0, 1, 0, 1, 1, 1,
0, 0, 0, 0, 1, 1, 1, 0, 0, 1, 0, 0, 0, 0, 1, 1, 1, 1, 0, 1, 0, 1,
1, 1, 0, 1, 1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 0, 0, 0,
0, 0, 1, 0, 0, 0, 1, 0, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1, 0, 0, 1, 0,
1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 1,
1, 0, 1, 0, 1, 1, 0, 0, 0, 1, 0, 1, 1, 1, 0, 0, 1, 1, 0, 0, 0, 1,
1, 1, 0, 1, 0, 1, 1, 1, 1, 0, 1, 0, 0, 1, 0, 0, 1, 0, 1, 0, 1, 1,
0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 1, 1, 0, 1, 0, 0, 0, 1, 1, 1,
1, 0, 0, 1, 0, 0, 0, 1, 0, 1, 0, 0, 1, 0, 1, 0, 1, 0, 0, 1, 0, 0,
0, 0, 0, 0, 1, 0, 0, 0, 1, 1, 1, 0, 1, 1, 0, 1, 1, 0, 1, 0, 0, 0,
1, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1, 1, 0, 1, 1, 0, 0, 0, 1, 0, 0, 1,
0, 0, 0, 0, 0, 1, 1, 0, 0, 1, 1, 1, 1, 0, 1, 0, 1, 0, 1, 1, 1, 1,
1, 0, 1, 0, 0, 0, 1, 0, 0, 1, 0, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 0,
0, 0, 0, 0, 1, 0, 1, 1, 1, 0, 1, 1, 1, 1, 0, 0, 0, 0, 0, 1, 1, 1,
1, 1, 1, 1, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 1, 0, 1, 0, 1,
1, 0, 1, 1, 1, 0, 0, 1, 0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 0, 0, 1, 1,
0, 0, 0, 1, 1, 1, 1, 1, 0, 1, 1, 0, 1, 0, 0, 0, 1, 1, 0, 1, 1, 0,
1, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 1, 1, 1, 0, 1, 1, 1, 0,
0, 0, 0, 0, 0, 1, 1, 1, 1, 0, 1, 0, 1, 1, 0, 1, 0, 1, 1, 1, 0, 0,
0, 0, 1, 1, 1, 0, 1, 0, 1, 0, 0, 1, 0, 1, 0, 0, 0, 1, 1, 1, 0, 1,
0, 1, 1, 1, 0, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 0, 0, 1, 0,
0, 1, 1, 1, 0, 1, 1, 0, 0, 1, 1, 0, 1, 1, 0, 1, 1, 1, 0, 1, 1, 0,
1, 1, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 1, 1, 1, 0, 1, 1, 0,
0, 1, 0, 0, 1, 1, 0, 1, 0, 0, 1, 0, 0, 1, 0, 1, 0, 1, 1, 1, 0, 0,
0, 0, 1, 1, 0, 1, 0, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 0, 1,
1, 0, 1, 1, 0, 1, 1, 0, 1, 0, 0, 1, 0, 0, 0, 1, 0, 1, 0, 1, 1, 0,
1, 1, 1, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1, 0, 0, 1, 0, 1, 1, 0, 0,
1, 0, 1, 1, 1, 1, 1, 1, 1, 0, 1, 0, 0, 0, 1, 0, 0, 1, 1, 1, 0, 1,
1, 1, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 1, 1, 0, 1, 1, 0, 0, 1, 1, 0,
1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 1, 0, 0, 1, 1, 0, 1,
1, 1, 1, 0, 0, 1, 1, 1, 0, 1, 0, 0, 1, 1, 0, 1, 1, 1, 1, 1, 1, 0,
1, 1, 1, 0, 0, 1, 1, 0, 0, 1, 0, 0, 1, 1, 0, 0, 0, 1, 0, 1, 1, 1,
0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 0, 1, 0, 0],
dtype=uint8)
tagUsando Cuantización Binaria en Qdrant
También puede usar la biblioteca de integración de Qdrant para poner embeddings binarios directamente en su almacén de vectores Qdrant. Como Qdrant ha implementado internamente BinaryQuantization, puede usarlo como una configuración preestablecida para toda la colección de vectores, permitiéndole recuperar y almacenar vectores binarios sin ningún otro cambio en su código.
Vea el código de ejemplo a continuación para saber cómo:
import qdrant_client
import requests
from qdrant_client.models import Distance, VectorParams, Batch, BinaryQuantization, BinaryQuantizationConfig
# Proporciona la clave API de Jina y elige uno de los modelos disponibles.
# Puedes obtener una clave de prueba gratuita aquí: https://jina.ai/embeddings/
JINA_API_KEY = "jina_xxx"
MODEL = "jina-embeddings-v2-base-en" # o "jina-embeddings-v2-base-en"
EMBEDDING_SIZE = 768 # 512 para la variante pequeña
# Obtener embeddings desde la API
url = "https://api.jina.ai/v1/embeddings"
headers = {
"Content-Type": "application/json",
"Authorization": f"Bearer {JINA_API_KEY}",
}
text_to_encode = ["Tu texto va aquí", "Puedes enviar múltiples textos"]
data = {
"input": text_to_encode,
"model": MODEL,
}
response = requests.post(url, headers=headers, json=data)
embeddings = [d["embedding"] for d in response.json()["data"]]
# Indexar los embeddings en Qdrant
client = qdrant_client.QdrantClient(":memory:")
client.create_collection(
collection_name="MyCollection",
vectors_config=VectorParams(size=EMBEDDING_SIZE, distance=Distance.DOT, on_disk=True),
quantization_config=BinaryQuantization(binary=BinaryQuantizationConfig(always_ram=True)),
)
client.upload_collection(
collection_name="MyCollection",
ids=list(range(len(embeddings))),
vectors=embeddings,
payload=[
{"text": x} for x in text_to_encode
],
)Para configurar la búsqueda, debes usar los parámetros oversampling y rescore:
from qdrant_client.models import SearchParams, QuantizationSearchParams
results = client.search(
collection_name="MyCollection",
query_vector=embeddings[0],
search_params=SearchParams(
quantization=QuantizationSearchParams(
ignore=False,
rescore=True,
oversampling=2.0,
)
)
)tagUso de LlamaIndex
Para usar embeddings binarios de Jina con LlamaIndex, establece el parámetro encoding_queries como binary al instanciar el objeto JinaEmbedding:
from llama_index.embeddings.jinaai import JinaEmbedding
# Puedes obtener una clave de prueba gratuita en https://jina.ai/embeddings/
JINA_API_KEY = "<TU CLAVE API>"
jina_embedding_model = JinaEmbedding(
api_key=jina_ai_api_key,
model="jina-embeddings-v2-base-en",
encoding_queries='binary',
encoding_documents='float'
)
jina_embedding_model.get_query_embedding('Texto de consulta aquí')
jina_embedding_model.get_text_embedding_batch(['X', 'Y', 'Z'])
tagOtras Bases de Datos Vectoriales que Soportan Embeddings Binarios
Las siguientes bases de datos vectoriales proporcionan soporte nativo para vectores binarios:
tagEjemplo
Para mostrarte los embeddings binarios en acción, tomamos una selección de resúmenes de arXiv.org, y obtuvimos tanto vectores de punto flotante de 32 bits como vectores binarios usando jina-embeddings-v2-base-en. Luego los comparamos con los embeddings de una consulta de ejemplo: "3D segmentation".
Puedes ver en la tabla siguiente que las tres primeras respuestas son las mismas y cuatro de las cinco principales coinciden. El uso de vectores binarios produce coincidencias casi idénticas en los primeros resultados.
| Binary | 32-bit Float | |||
|---|---|---|---|---|
| Rank | Hamming dist. |
Matching Text | Cosine | Matching text |
| 1 | 0.1862 | SEGMENT3D: A Web-based Application for Collaboration... |
0.2340 | SEGMENT3D: A Web-based Application for Collaboration... |
| 2 | 0.2148 | Segmentation-by-Detection: A Cascade Network for... |
0.2857 | Segmentation-by-Detection: A Cascade Network for... |
| 3 | 0.2174 | Vox2Vox: 3D-GAN for Brain Tumour Segmentation... |
0.2973 | Vox2Vox: 3D-GAN for Brain Tumour Segmentation... |
| 4 | 0.2318 | DiNTS: Differentiable Neural Network Topology Search... |
0.2983 | Anisotropic Mesh Adaptation for Image Segmentation... |
| 5 | 0.2331 | Data-Driven Segmentation of Post-mortem Iris Image... |
0.3019 | DiNTS: Differentiable Neural Network Topology... |