¿Pueden los modelos de Embedding/Reranker comparar números?

Esta fue una pregunta que me hicieron hoy en la conferencia ICML en Viena.

Durante el descanso para el café, un usuario de Jina se me acercó con una pregunta que surgió de discusiones recientes en la comunidad de LLM. Me preguntó si nuestro modelo de embeddings podía determinar que 9.11 es menor que 9.9, una tarea donde muchos LLMs dicen lo contrario.

"Honestamente, no lo sé", respondí. Mientras él explicaba la importancia de esta capacidad para su aplicación y sugería que la tokenización podría ser la raíz del problema, me encontré asintiendo - mi mente ya estaba corriendo con ideas para un experimento para descubrir la respuesta.

En este artículo, quiero probar si nuestro modelo de embeddings, jina-embeddings-v2-base-en (lanzado en octubre de 2023), y el Reranker, jina-reranker-v2-multilingual (lanzado en junio de 2024), pueden comparar números con precisión. Para extender el alcance más allá de la simple comparación de 9.11 y 9.9, he diseñado un conjunto de experimentos que incluyen varios tipos de números: enteros pequeños, números grandes, decimales, números negativos, moneda, fechas y horas. El objetivo es evaluar la efectividad de nuestros modelos en el manejo de diferentes formatos numéricos.

tagConfiguración Experimental

La implementación completa se puede encontrar en el Colab a continuación:

El diseño del experimento es bastante sencillo. Por ejemplo, para verificar si el modelo de embeddings entiende números entre [1, 100]. Los pasos son los siguientes:

Construir Documentos: Generar documentos de "literales de cadena" para cada número desde 1 hasta 100.
Enviar a la API de Embeddings: Usar la API de Embeddings para obtener embeddings para cada documento.
Calcular Similitud del Coseno: Calcular la similitud del coseno por pares para cada dos documentos para crear una matriz de similitud.
Hacer Gráfico de Dispersión: Visualizar los resultados usando un gráfico de dispersión. Cada elemento $(i, j)$ en la matriz de similitud se mapea a un punto con: Eje X: $(i - j)$ ; Eje Y: el valor de similitud de $(i, j)$

Si el delta $(i - j)$ es cero, es decir, $i = j$ , entonces la similitud semántica debería ser la más alta. A medida que el delta $(i - j)$ aumenta, la similitud debería disminuir. Idealmente, la similitud debería ser linealmente proporcional al valor delta. Si no podemos observar tal linealidad, entonces es probable que el modelo no pueda entender los números y pueda producir errores como que 9.11 es mayor que 9.9.

El modelo Reranker sigue un procedimiento similar. La diferencia clave es que iteramos a través de los documentos construidos, estableciendo cada uno como query anteponiendo el prompt "what is the closest item to..." y clasificando todos los demás como documents. La puntuación de relevancia devuelta por la API del Reranker se usa directamente como medida de similitud semántica. La implementación central se ve así.

def rerank_documents(documents):
    reranker_url = "https://api.jina.ai/v1/rerank"
    headers = {
        "Content-Type": "application/json",
        "Authorization": f"Bearer {token}"
    }

    # Initialize similarity matrix
    similarity_matrix = np.zeros((len(documents), len(documents)))

    for idx, d in enumerate(documents):
        payload = {
            "model": "jina-reranker-v2-base-multilingual",
            "query": f"what is the closest item to {d}?",
            "top_n": len(documents),
            "documents": documents
        }
    ...

tag¿Pueden los Modelos Comparar Números Entre [1, 2, 3, ..., 100]?

Gráfico de dispersión con media y varianza en cada delta. Izquierda: jina-embeddings-v2-base-en; Derecha: jina-reranker-v2-multilingual. documents = [str(i) for i in range(1, 101)]

tagCómo Leer Estos Gráficos

Antes de continuar con más experimentos, permítanme primero explicar cómo leer correctamente estos gráficos. En primer lugar, mi observación de los dos gráficos anteriores es que el modelo de embeddings funciona bien, mientras que el modelo reranker no lo hace tan bien. Entonces, ¿qué estamos viendo y por qué?

El eje X representa el delta de los índices $(i,j)$ , o $i-j$ , cuando muestreamos uniformemente $d_i$ y $d_j$ de nuestros conjuntos de documentos. Este delta varía de $[-100, 100]$ . Dado que nuestro conjunto de documentos está ordenado por construcción, es decir, cuanto menor sea $|i-j|$ , más cercanos son semánticamente $d_i$ y $d_j$ ; cuanto más alejados estén $i$ y $j$ , menor será la similitud entre $d_i$ y $d_j$ . Por eso ves que la similitud (representada por el eje Y) se dispara en $X=0$ y luego cae linealmente al moverte a izquierda y derecha.

Idealmente, esto debería crear un pico pronunciado o una forma de "flecha hacia arriba" como ^. Sin embargo, ese no es siempre el caso. Si fijas el eje X en un punto, digamos $X=25$ , y miras a lo largo del eje Y, encontrarás valores de similitud que van de 0.80 a 0.95. Eso significa que $\mathrm{sim}(d_27, d_2)$ puede ser 0.81 mientras que $\mathrm{sim}(d_42, d_17)$ puede ser 0.91 a pesar de que sus deltas son todos 25.

La línea de tendencia cian muestra la similitud media en cada valor X con la desviación estándar. Además, nota que la similitud debería caer linealmente porque nuestro conjunto de documentos está espaciado uniformemente, asegurando intervalos iguales entre documentos contiguos.

Ten en cuenta que los gráficos de embeddings serán siempre simétricos, con el valor Y más grande de 1.0 en $X=0$ . Esto es porque la similitud del coseno es simétrica para $d_i$ y $d_j$ , y $\cos(0)=1$ .

Por otro lado, los gráficos del reranker son siempre asimétricos debido a los diferentes roles de la consulta y los documentos en el modelo reranker. El valor máximo probablemente no sea 1.0 porque $X=0$ significa que usamos el reranker para calcular la puntuación de relevancia de "what is the closest item to 4" vs "4". Si lo piensas, no hay garantía de que $X=0$ lleve al valor Y máximo.

tag¿Pueden los Modelos Comparar Números Negativos Entre [-100, -99, -98, ..., -1]?

Gráfico de dispersión con media y varianza en cada delta. Izquierda: jina-embeddings-v2-base-en; Derecha: jina-reranker-v2-multilingual. Aquí queremos probar si el modelo puede determinar la similitud semántica en el espacio negativo. documents = [str(-i) for i in range(1, 101)]

tag¿Pueden los Modelos Comparar Números con Intervalos Más Grandes [1000, 2000, 3000, ..., 100000]?

Aquí queremos probar si el modelo puede determinar la similitud semántica cuando comparamos números con un intervalo de 1000. documents = [str(i*1000) for i in range(1, 101)] Gráfico de dispersión con media y varianza en cada delta. Izquierda: jina-embeddings-v2-base-en; Derecha: jina-reranker-v2-multilingual.

tag¿Pueden los Modelos Comparar Números de un Rango Arbitrario, por ejemplo [376, 377, 378, ..., 476]?

Aquí queremos probar si el modelo puede determinar la similitud semántica cuando comparamos números en un rango arbitrario, así que movemos los números a un rango aleatorio documents = [str(i+375) for i in range(1, 101)]. Gráfico de dispersión con media y varianza en cada delta. Izquierda: jina-embeddings-v2-base-en; Derecha: jina-reranker-v2-multilingual.

tag¿Pueden los Modelos Comparar Números Grandes Entre [4294967296, 4294967297, 4294967298, ..., 4294967396]?

Aquí queremos probar si el modelo puede determinar la similitud semántica cuando comparamos números muy grandes. Similar a la idea del último experimento, movemos el rango más allá a un número grande. documents = [str(i+4294967296) for i in range(1, 101)] Gráfico de dispersión con media y varianza en cada delta. Izquierda: jina-embeddings-v2-base-en; Derecha: jina-reranker-v2-multilingual.

tag¿Pueden los Modelos Comparar Números Decimales Entre [0.0001, 0.0002, 0.0003, ...,0.1]? (sin dígitos fijos)

Aquí queremos probar si el modelo puede determinar la similitud semántica cuando comparamos decimales. documents = [str(i/1000) for i in range(1, 101)] Gráfico de dispersión con media y varianza en cada delta. Izquierda: jina-embeddings-v2-base-en; Derecha: jina-reranker-v2-multilingual.

tag¿Pueden los Modelos Comparar Números de Moneda Entre [ $1,$ 2, $3, ...,$ 100]?

Aquí queremos probar si el modelo puede determinar la similitud semántica cuando comparamos números en formato de moneda. documents = ['$'+str(i) for i in range(1, 101)] Gráfico de dispersión con media y varianza en cada delta. Izquierda: jina-embeddings-v2-base-en; Derecha: jina-reranker-v2-multilingual.

tag¿Pueden los Modelos Comparar Fechas Entre [2024-07-24, 2024-07-25, 2024-07-26, ..., 2024-10-31]?

Aquí queremos probar si el modelo puede determinar la similitud semántica cuando comparamos números en formato de fecha, es decir, AAAA-MM-DD. today = datetime.today(); documents = [(today + timedelta(days=i)).strftime('%Y-%m-%d') for i in range(100)] Gráfico de dispersión con media y varianza en cada delta. Izquierda: jina-embeddings-v2-base-en; Derecha: jina-reranker-v2-multilingual.

tag¿Pueden los Modelos Comparar Horas Entre [19:00:07, 19:00:08, 19:00:09,..., 20:39:07]?

Aquí queremos probar si el modelo puede detectar la similitud semántica cuando comparamos números en formato de tiempo, es decir, hh:mm:ss. now = datetime.now(); documents = [(now + timedelta(minutes=i)).strftime('%H:%M:%S') for i in range(100)] Gráfico de dispersión con media y varianza en cada delta. Izquierda: jina-embeddings-v2-base-en; Derecha: jina-reranker-v2-multilingual.

tagObservaciones

Aquí hay algunas observaciones de los gráficos anteriores:

tagModelos Reranker

Los modelos reranker tienen dificultades para comparar números. Incluso en el caso más simple de comparar números entre [1, 100], su rendimiento es deficiente.
Es importante notar la construcción especial de prompt utilizada para las consultas en nuestro uso del reranker, es decir, what is the closest item to x, ya que esto también puede impactar los resultados.

tagModelos de Embedding

Los modelos de embedding tienen un rendimiento razonablemente bueno al comparar números enteros pequeños en el rango [1, 100] o números negativos en [-100, 1]. Sin embargo, su rendimiento se degrada significativamente al desplazar este intervalo a otros valores, agregar más intervalos o tratar con flotantes más grandes o más pequeños.
Se pueden observar picos regulares en ciertos intervalos, generalmente cada 10 pasos. Este comportamiento puede estar relacionado con cómo el tokenizer procesa las cadenas, potencialmente tokenizando una cadena en "10" o "1" y "0".

tagComprensión de Fecha y Hora

Curiosamente, los modelos de embedding parecen tener una buena comprensión de fechas y horas, comparándolas correctamente la mayoría del tiempo. Para los gráficos de fechas, aparecen picos cada 30/31 pasos, correspondientes al número de días en un mes. Para los gráficos de tiempo, aparecen picos cada 60 pasos, correspondientes a los minutos en una hora.
Los modelos reranker también parecen captar esta comprensión hasta cierto punto.

tagVisualización de la Similitud con "Cero"

Actualizado el 29 de julio de 2024

Otro experimento interesante, que es probablemente más intuitivo, es visualizar directamente la puntuación de similitud o relevancia entre cualquier número y cero (es decir, el origen). Al fijar el punto de referencia como el embedding de cero, queremos ver si la similitud semántica disminuye linealmente a medida que los números se hacen más grandes. Para el reranker, podemos fijar la consulta a "0" o "What is the closest number to number zero?" y clasificar todos los números para ver si sus puntuaciones de relevancia disminuyen a medida que los números aumentan. Los resultados se muestran a continuación:

Aquí, fijamos el "embedding de origen" al embedding de "cero" y comprobamos si la similitud semántica entre cualquier número y cero es proporcional al valor del número. Específicamente, usamos documents = [str(i) for i in range(2048)]. Se muestra el gráfico de dispersión con media y varianza para cada delta. Izquierda: jina-embeddings-v2-base-en; Derecha: jina-reranker-v2-multilingual.

tagConclusión

Este artículo ilustra cómo nuestros modelos actuales de embedding y reranker manejan las comparaciones numéricas. A pesar de la configuración experimental relativamente simple, expone algunas fallas fundamentales en los modelos actuales y proporciona información valiosa para el desarrollo de nuestro próximo embedding y reranker.

Dos factores clave determinan si un modelo puede comparar números con precisión:

Primero, la tokenización: Si el vocabulario solo incluye dígitos 0-9, entonces 11 podría tokenizarse en tokens separados 1 y 1, o como un solo token 11. Esta elección impacta la comprensión del modelo de los valores numéricos.

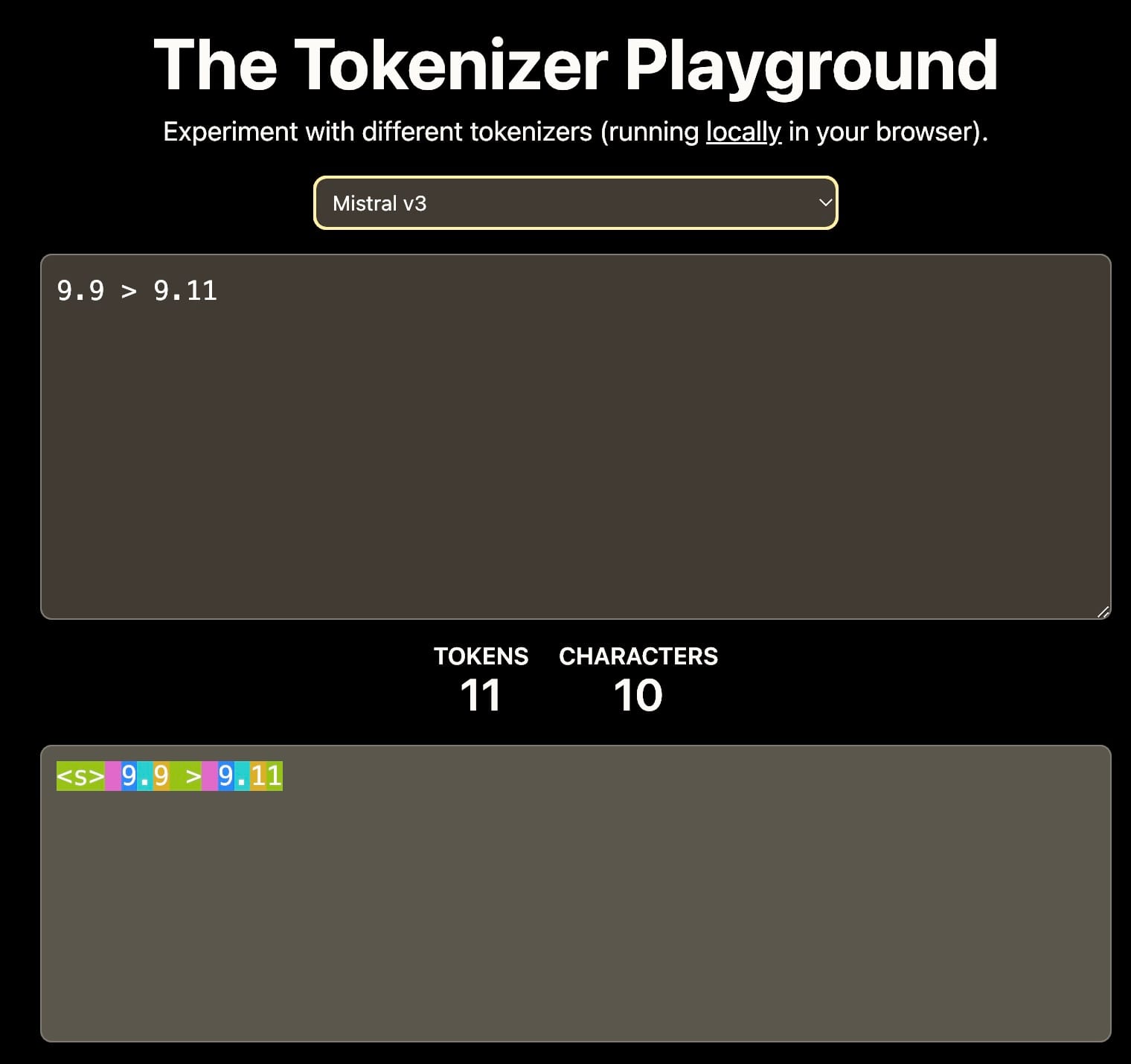
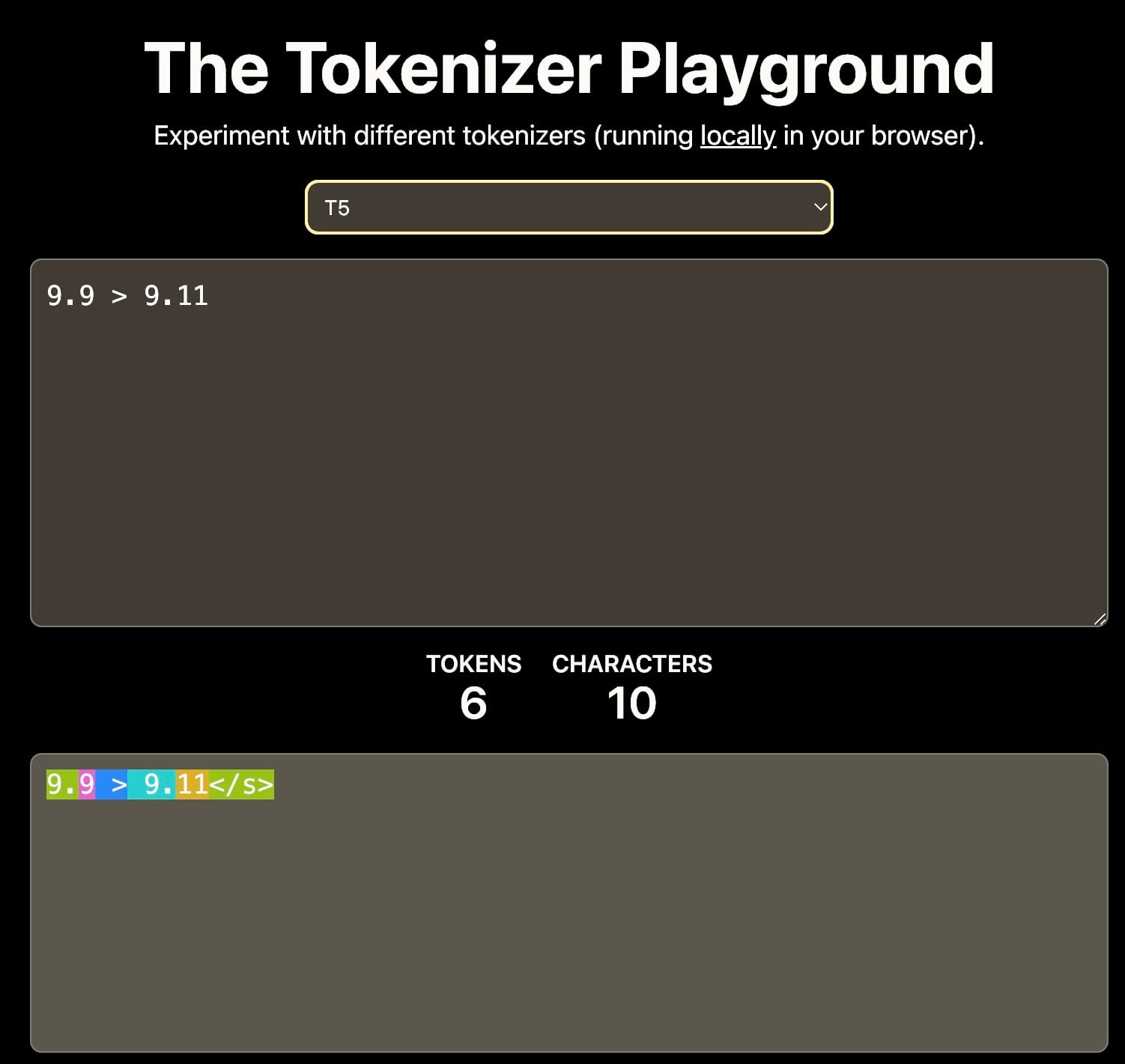
Diferentes tokenizers resultan en diferentes interpretaciones de 9.11. Esto puede afectar el aprendizaje contextual posterior. Fuente: The Tokenizer Playground en HuggingFace.

Segundo, los datos de entrenamiento: El corpus de entrenamiento influye significativamente en las capacidades de razonamiento numérico del modelo. Por ejemplo, si los datos de entrenamiento incluyen principalmente documentación de software o repositorios de GitHub donde el versionado semántico es común, el modelo podría interpretar que 9.11 es mayor que 9.9, ya que 9.11 es la versión menor que sigue a 9.9.

La capacidad aritmética de los modelos de recuperación densa, como embeddings y rerankers, es crucial para tareas que involucran RAG y recuperación y razonamiento avanzados. Las fuertes capacidades de razonamiento numérico pueden mejorar significativamente la calidad de búsqueda, particularmente cuando se trata de datos estructurados como JSON.