Plongements binaires : Toute l'IA, 3,125 % du volume

Les embeddings sont devenus la pierre angulaire d'une variété d'applications d'IA et de traitement du langage naturel, offrant un moyen de représenter le sens des textes sous forme de vecteurs de haute dimension. Cependant, avec l'augmentation de la taille des modèles et des quantités croissantes de données traitées par les modèles d'IA, les exigences en matière de calcul et de stockage pour les embeddings traditionnels ont augmenté. Les embeddings binaires ont été introduits comme une alternative compacte et efficace qui maintient des performances élevées tout en réduisant drastiquement les besoins en ressources.

Les embeddings binaires sont une façon d'atténuer ces exigences en ressources en réduisant la taille des vecteurs d'embedding jusqu'à 96 % (96,875 % dans le cas des Jina Embeddings). Les utilisateurs peuvent exploiter la puissance des embeddings binaires compacts dans leurs applications d'IA avec une perte minimale de précision.

tagQue Sont les Embeddings Binaires ?

Les embeddings binaires sont une forme spécialisée de représentation des données où les vecteurs traditionnels à virgule flottante de haute dimension sont transformés en vecteurs binaires. Cela permet non seulement de compresser les embeddings mais aussi de conserver presque toute l'intégrité et l'utilité des vecteurs. L'essence de cette technique réside dans sa capacité à maintenir la sémantique et les distances relationnelles entre les points de données même après conversion.

La magie derrière les embeddings binaires est la quantification, une méthode qui transforme des nombres de haute précision en nombres de précision inférieure. Dans la modélisation IA, cela signifie souvent convertir les nombres à virgule flottante 32 bits des embeddings en représentations avec moins de bits, comme des entiers 8 bits.

Comparison of Hokusai's Great Wave print in color and black & white, highlighting the wave's dynamism and detail. — La binarisation est la transformation de toutes les valeurs scalaires en 0 ou 1, comme la conversion d'une image couleur en une image avec uniquement des pixels noirs ou blancs. Image : 神奈川沖浪裏 (1831) par 葛飾 (Hokusai)

Les embeddings binaires poussent cela à l'extrême, réduisant chaque valeur à 0 ou 1. La transformation des nombres à virgule flottante 32 bits en chiffres binaires réduit la taille des vecteurs d'embedding d'un facteur 32, soit une réduction de 96,875 %. Les opérations vectorielles sur les embeddings résultants sont beaucoup plus rapides. L'utilisation d'accélérations matérielles disponibles sur certaines puces peut augmenter la vitesse des comparaisons vectorielles bien au-delà d'un facteur 32 lorsque les vecteurs sont binarisés.

Certaines informations sont inévitablement perdues durant ce processus, mais cette perte est minimisée lorsque le modèle est très performant. Si les embeddings non quantifiés de différentes choses sont maximalement différents, alors la binarisation est plus susceptible de bien préserver cette différence. Sinon, il peut être difficile d'interpréter correctement les embeddings.

Les modèles Jina Embeddings sont entraînés pour être très robustes exactement de cette manière, les rendant bien adaptés à la binarisation.

De tels embeddings compacts rendent possibles de nouvelles applications d'IA, particulièrement dans des contextes aux ressources limitées comme les utilisations mobiles et sensibles au temps.

Ces avantages en termes de coûts et de temps de calcul s'accompagnent d'un coût de performance relativement faible, comme le montre le graphique ci-dessous.

*NDCG@10 : Scores calculés en utilisant le* *Normalized Discounted Cumulative Gain* *pour les 10 premiers résultats.*

Pour jina-embeddings-v2-base-en, la quantification binaire réduit la précision de récupération de 47,13 % à 42,05 %, une perte d'environ 10 %. Pour jina-embeddings-v2-base-de, cette perte n'est que de 4 %, passant de 44,39 % à 42,65 %.

Les modèles Jina Embeddings performent si bien lors de la production de vecteurs binaires car ils sont entraînés pour créer une distribution plus uniforme des embeddings. Cela signifie que deux embeddings différents seront probablement plus éloignés l'un de l'autre dans plus de dimensions que les embeddings d'autres modèles. Cette propriété garantit que ces distances sont mieux représentées par leurs formes binaires.

tagComment Fonctionnent les Embeddings Binaires ?

Pour comprendre comment cela fonctionne, considérons trois embeddings : A, B, et C. Ces trois sont tous des vecteurs à virgule flottante complets, non binarisés. Maintenant, disons que la distance de A à B est supérieure à la distance de B à C. Avec les embeddings, nous utilisons typiquement la distance cosinus, donc :

$\cos(A,B) > \cos(B,C)$

Si nous binarisons A, B, et C, nous pouvons mesurer la distance plus efficacement avec la distance de Hamming.

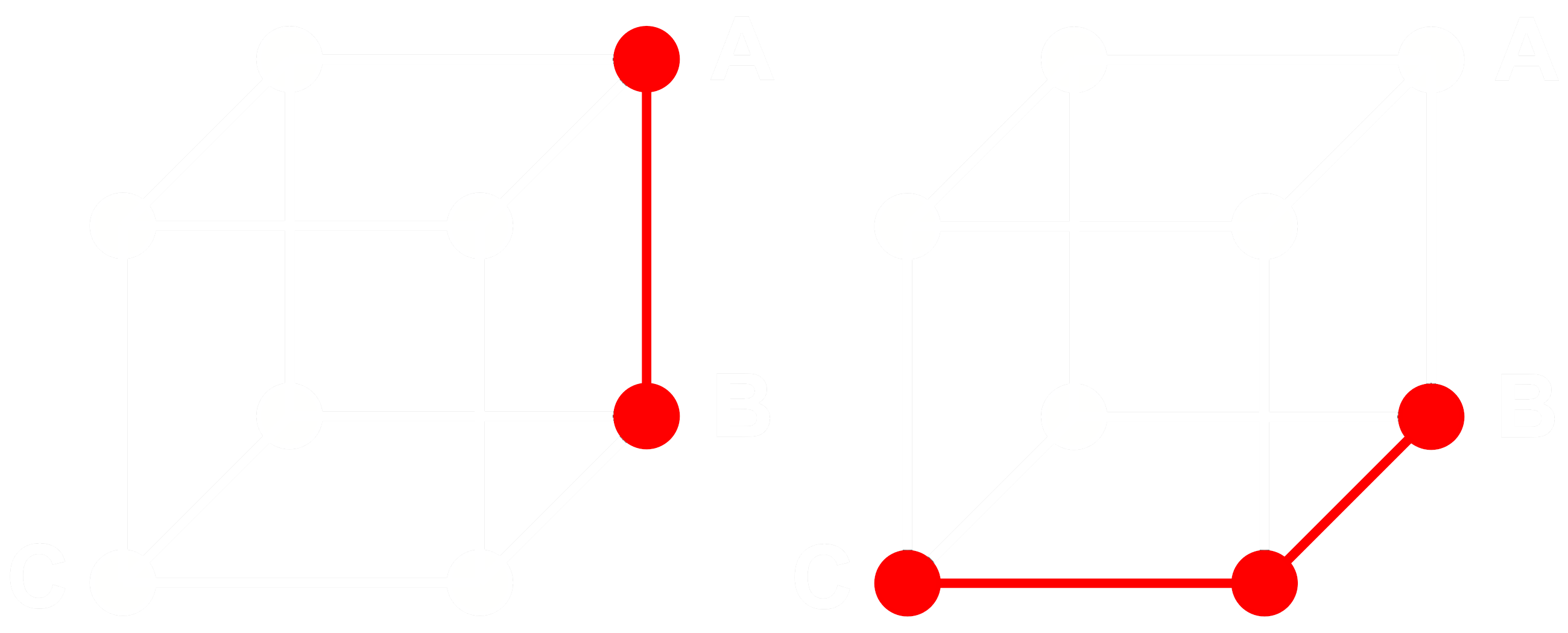
Geometric diagrams with labeled circles A, B, and C connected by lines against a contrasting background. — Distance de Hamming sur un cube. Gauche : Distance de A à B est 1. Droite : Distance de B à C est 2.

Appelons A_bin, B_bin et C_bin les versions binarisées de A, B et C.

Pour les vecteurs binaires, si la distance cosinus entre A_bin et B_bin est supérieure à celle entre B_bin et C_bin, alors la distance de Hamming entre A_bin et B_bin est supérieure ou égale à la distance de Hamming entre B_bin et C_bin.

Donc si :

$\cos(A,B) > \cos(B,C)$

alors pour les distances de Hamming :

$hamm(A{bin}, B{bin}) \geq hamm(B{bin}, C{bin})$

Idéalement, lorsque nous binarisons les embeddings, nous voulons que les mêmes relations avec les embeddings complets s'appliquent aux embeddings binaires. Cela signifie que si une distance est supérieure à une autre pour le cosinus à virgule flottante, elle devrait être supérieure pour la distance de Hamming entre leurs équivalents binarisés :

$\cos(A,B) > \cos(B,C) \Rightarrow hamm(A{bin}, B{bin}) \geq hamm(B{bin}, C{bin})$

Nous ne pouvons pas rendre cela vrai pour tous les triplets d'embeddings, mais nous pouvons le rendre vrai pour presque tous.

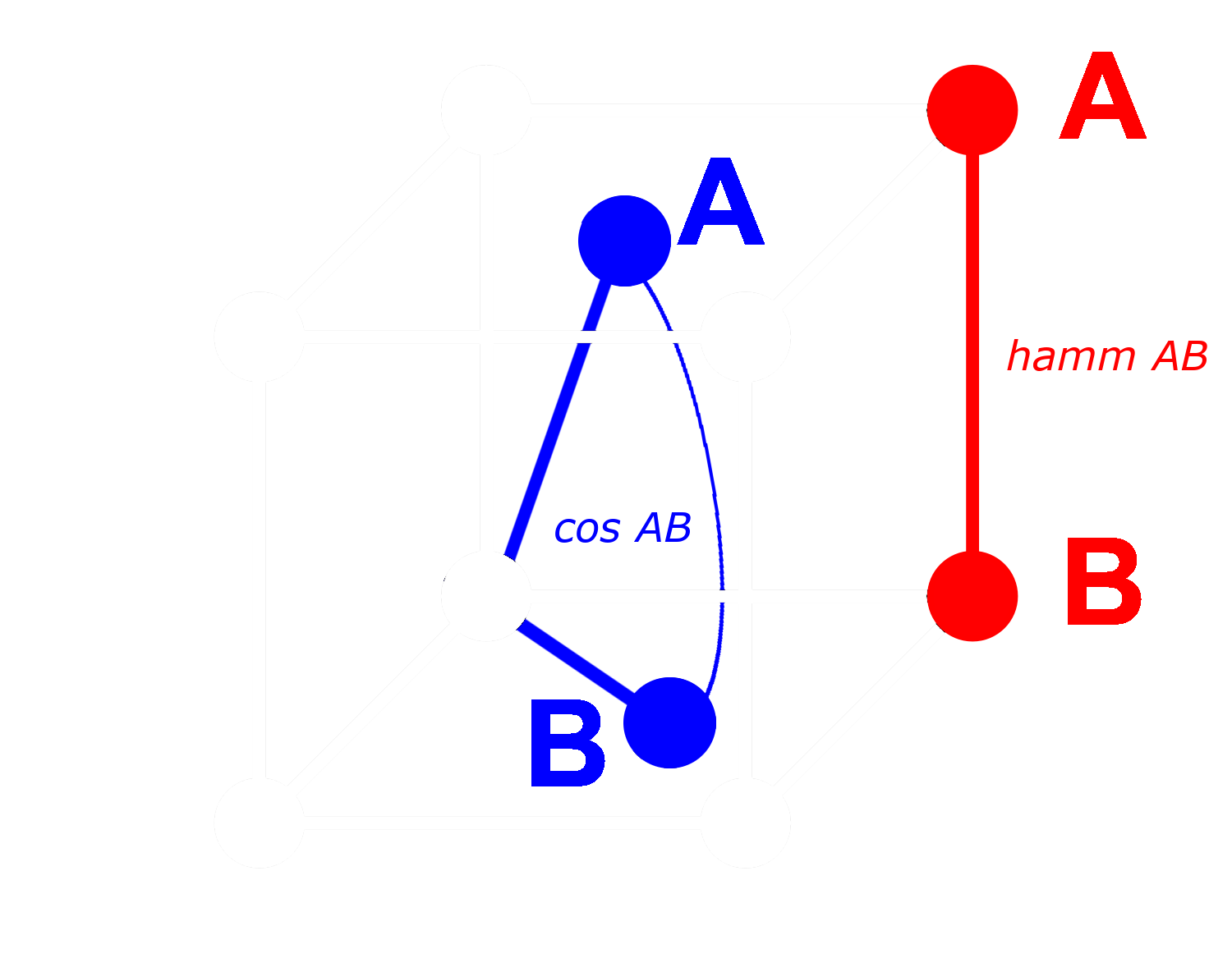
Graph with labeled points A and B, connected by lines marked as 'hamm AB' and 'cos AB', on a black background. — Les points bleus correspondent aux vecteurs à virgule flottante complets et les rouges à leurs équivalents binarisés.

Avec un vecteur binaire, nous pouvons traiter chaque dimension comme soit présente (un) soit absente (zéro). Plus deux vecteurs sont éloignés l'un de l'autre sous forme non binaire, plus la probabilité est élevée que dans une dimension donnée, l'un ait une valeur positive et l'autre une valeur négative. Cela signifie que sous forme binaire, il y aura très probablement plus de dimensions où l'un a un zéro et l'autre un un. Cela les rend plus éloignés selon la distance de Hamming.

L'inverse s'applique aux vecteurs qui sont plus proches : Plus les vecteurs non binaires sont proches, plus la probabilité est élevée que dans toute dimension, les deux aient des zéros ou des uns. Cela les rend plus proches selon la distance de Hamming.

Les modèles Jina Embeddings sont si bien adaptés à la binarisation car nous les entraînons en utilisant l'extraction négative et d'autres pratiques d'ajustement fin pour augmenter particulièrement la distance entre les choses dissemblables et réduire la distance entre les choses similaires. Cela rend les embeddings plus robustes, plus sensibles aux similitudes et aux différences, et rend la distance de Hamming entre les embeddings binaires plus proportionnelle à la distance cosinus entre les non binaires.

tagCombien Puis-je Économiser avec les Embeddings Binaires de Jina AI ?

L'adoption des modèles d'embedding binaires de Jina AI ne réduit pas seulement la latence dans les applications sensibles au temps, mais génère également des avantages considérables en termes de coûts, comme le montre le tableau ci-dessous :

Modèle	Mémoire pour 250 millions d'embeddings	Moyenne des benchmarks de récupération	Prix estimé sur AWS (3,8 $ par GB/mois avec instances x2gb)
Embeddings à virgule flottante 32 bits	715 GB	47,13	35 021 $
Embeddings binaires	22,3 GB	42,05	1 095 $

Ces économies de plus de 95 % ne s'accompagnent que d'une réduction d'environ 10 % de la précision de recherche.

Ces économies sont encore plus importantes que l'utilisation de vecteurs binarisés du modèle Ada 2 d'OpenAI ou de Embed v3 de Cohere, qui produisent tous deux des embeddings de sortie de 1024 dimensions ou plus. Les embeddings de Jina AI n'ont que 768 dimensions tout en offrant des performances comparables aux autres modèles, les rendant plus petits même avant la quantification pour une précision équivalente.

💡

Les vecteurs binaires économisent la mémoire, le temps de calcul, la bande passante de transmission et l'espace disque, offrant des avantages financiers dans plusieurs catégories.

Ces économies sont également environnementales, utilisant moins de matériaux rares et moins d'énergie.

tagPour Commencer

Pour obtenir des embeddings binaires en utilisant l'API Jina Embeddings, il suffit d'ajouter le paramètre encoding_type à votre appel API, avec la valeur binary pour obtenir l'embedding binarisé encodé en entiers signés, ou ubinary pour les entiers non signés.

tagAccès Direct à l'API Jina Embedding

Utilisation de curl :

curl https://api.jina.ai/v1/embeddings \
  -H "Content-Type: application/json" \
  -H "Authorization: Bearer <YOUR API KEY>" \
  -d '{
    "input": ["Your text string goes here", "You can send multiple texts"],
    "model": "jina-embeddings-v2-base-en",
    "encoding_type": "binary"
  }'

Ou via l'API Python requests :

import requests

headers = {
  "Content-Type": "application/json",
  "Authorization": "Bearer <YOUR API KEY>"
}

data = {
  "input": ["Your text string goes here", "You can send multiple texts"],
  "model": "jina-embeddings-v2-base-en",
  "encoding_type": "binary",
}

response = requests.post(
    "https://api.jina.ai/v1/embeddings", 
    headers=headers, 
    json=data,
)

Avec la requête Python ci-dessus, vous obtiendrez la réponse suivante en inspectant response.json() :

{
  "model": "jina-embeddings-v2-base-en",
  "object": "list",
  "usage": {
    "total_tokens": 14,
    "prompt_tokens": 14
  },
  "data": [
    {
      "object": "embedding",
      "index": 0,
      "embedding": [
        -0.14528547,
        -1.0152762,
        ...
      ]
    },
    {
      "object": "embedding",
      "index": 1,
      "embedding": [
        -0.109809875,
        -0.76077706,
        ...
      ]
    }
  ]
}

Ce sont deux vecteurs d'embedding binaires stockés sous forme de 96 entiers signés sur 8 bits. Pour les décompresser en 768 valeurs de 0 et 1, vous devez utiliser la bibliothèque numpy :

import numpy as np

# assign the first vector to embedding0
embedding0 = response.json()['data'][0]['embedding']

# convert embedding0 to a numpy array of unsigned 8-bit ints
uint8_embedding = np.array(embedding0).astype(numpy.uint8) 

# unpack to binary
np.unpackbits(uint8_embedding)

Le résultat est un vecteur de 768 dimensions ne contenant que des 0 et des 1 :

array([0, 0, 1, 1, 0, 1, 1, 0, 1, 1, 0, 0, 0, 1, 0, 1, 1, 1, 1, 1, 0, 0,
       0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 1, 1, 0, 0, 0, 1, 1, 1, 0, 1, 0, 1,
       0, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 1, 1, 0, 0, 0, 0, 1, 0, 1, 1, 1,
       0, 0, 0, 0, 1, 1, 1, 0, 0, 1, 0, 0, 0, 0, 1, 1, 1, 1, 0, 1, 0, 1,
       1, 1, 0, 1, 1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 0, 0, 0,
       0, 0, 1, 0, 0, 0, 1, 0, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1, 0, 0, 1, 0,
       1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 1,
       1, 0, 1, 0, 1, 1, 0, 0, 0, 1, 0, 1, 1, 1, 0, 0, 1, 1, 0, 0, 0, 1,
       1, 1, 0, 1, 0, 1, 1, 1, 1, 0, 1, 0, 0, 1, 0, 0, 1, 0, 1, 0, 1, 1,
       0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 1, 1, 0, 1, 0, 0, 0, 1, 1, 1,
       1, 0, 0, 1, 0, 0, 0, 1, 0, 1, 0, 0, 1, 0, 1, 0, 1, 0, 0, 1, 0, 0,
       0, 0, 0, 0, 1, 0, 0, 0, 1, 1, 1, 0, 1, 1, 0, 1, 1, 0, 1, 0, 0, 0,
       1, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1, 1, 0, 1, 1, 0, 0, 0, 1, 0, 0, 1,
       0, 0, 0, 0, 0, 1, 1, 0, 0, 1, 1, 1, 1, 0, 1, 0, 1, 0, 1, 1, 1, 1,
       1, 0, 1, 0, 0, 0, 1, 0, 0, 1, 0, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 0,
       0, 0, 0, 0, 1, 0, 1, 1, 1, 0, 1, 1, 1, 1, 0, 0, 0, 0, 0, 1, 1, 1,
       1, 1, 1, 1, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 1, 0, 1, 0, 1,
       1, 0, 1, 1, 1, 0, 0, 1, 0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 0, 0, 1, 1,
       0, 0, 0, 1, 1, 1, 1, 1, 0, 1, 1, 0, 1, 0, 0, 0, 1, 1, 0, 1, 1, 0,
       1, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 1, 1, 1, 0, 1, 1, 1, 0,
       0, 0, 0, 0, 0, 1, 1, 1, 1, 0, 1, 0, 1, 1, 0, 1, 0, 1, 1, 1, 0, 0,
       0, 0, 1, 1, 1, 0, 1, 0, 1, 0, 0, 1, 0, 1, 0, 0, 0, 1, 1, 1, 0, 1,
       0, 1, 1, 1, 0, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 0, 0, 1, 0,
       0, 1, 1, 1, 0, 1, 1, 0, 0, 1, 1, 0, 1, 1, 0, 1, 1, 1, 0, 1, 1, 0,
       1, 1, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 1, 1, 1, 0, 1, 1, 0,
       0, 1, 0, 0, 1, 1, 0, 1, 0, 0, 1, 0, 0, 1, 0, 1, 0, 1, 1, 1, 0, 0,
       0, 0, 1, 1, 0, 1, 0, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 0, 1,
       1, 0, 1, 1, 0, 1, 1, 0, 1, 0, 0, 1, 0, 0, 0, 1, 0, 1, 0, 1, 1, 0,
       1, 1, 1, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1, 0, 0, 1, 0, 1, 1, 0, 0,
       1, 0, 1, 1, 1, 1, 1, 1, 1, 0, 1, 0, 0, 0, 1, 0, 0, 1, 1, 1, 0, 1,
       1, 1, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 1, 1, 0, 1, 1, 0, 0, 1, 1, 0,
       1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 1, 0, 0, 1, 1, 0, 1,
       1, 1, 1, 0, 0, 1, 1, 1, 0, 1, 0, 0, 1, 1, 0, 1, 1, 1, 1, 1, 1, 0,
       1, 1, 1, 0, 0, 1, 1, 0, 0, 1, 0, 0, 1, 1, 0, 0, 0, 1, 0, 1, 1, 1,
       0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 0, 1, 0, 0],
      dtype=uint8)

tagUtilisation de la Quantification Binaire dans Qdrant

Vous pouvez également utiliser la bibliothèque d'intégration de Qdrant pour mettre directement les embeddings binaires dans votre base de vecteurs Qdrant. Comme Qdrant a implémenté en interne BinaryQuantization, vous pouvez l'utiliser comme configuration prédéfinie pour toute la collection de vecteurs, permettant de récupérer et stocker des vecteurs binaires sans autres modifications de votre code.

Voir le code d'exemple ci-dessous pour savoir comment faire :

import qdrant_client
import requests

from qdrant_client.models import Distance, VectorParams, Batch, BinaryQuantization, BinaryQuantizationConfig

# Fournir la clé API Jina et choisir l'un des modèles disponibles.
# Vous pouvez obtenir une clé d'essai gratuite ici : https://jina.ai/embeddings/
JINA_API_KEY = "jina_xxx"
MODEL = "jina-embeddings-v2-base-en"  # ou "jina-embeddings-v2-base-en"
EMBEDDING_SIZE = 768  # 512 pour la variante small

# Obtenir les embeddings depuis l'API
url = "https://api.jina.ai/v1/embeddings"

headers = {
    "Content-Type": "application/json",
    "Authorization": f"Bearer {JINA_API_KEY}",
}

text_to_encode = ["Your text string goes here", "You can send multiple texts"]
data = {
    "input": text_to_encode,
    "model": MODEL,
}

response = requests.post(url, headers=headers, json=data)
embeddings = [d["embedding"] for d in response.json()["data"]]


# Indexer les embeddings dans Qdrant
client = qdrant_client.QdrantClient(":memory:")
client.create_collection(
    collection_name="MyCollection",
    vectors_config=VectorParams(size=EMBEDDING_SIZE, distance=Distance.DOT, on_disk=True),
    quantization_config=BinaryQuantization(binary=BinaryQuantizationConfig(always_ram=True)),
)

client.upload_collection(
    collection_name="MyCollection",
    ids=list(range(len(embeddings))),
    vectors=embeddings,
    payload=[
            {"text": x} for x in text_to_encode
    ],
)

Pour configurer la recherche, vous devez utiliser les paramètres oversampling et rescore:

from qdrant_client.models import SearchParams, QuantizationSearchParams

results = client.search(
    collection_name="MyCollection",
    query_vector=embeddings[0],
    search_params=SearchParams(
        quantization=QuantizationSearchParams(
            ignore=False,
            rescore=True,
            oversampling=2.0,
        )
    )
)

tagUtilisation de LlamaIndex

Pour utiliser les embeddings binaires Jina avec LlamaIndex, définissez le paramètre encoding_queries sur binary lors de l'instanciation de l'objet JinaEmbedding :

from llama_index.embeddings.jinaai import JinaEmbedding

# Vous pouvez obtenir une clé d'essai gratuite sur https://jina.ai/embeddings/
JINA_API_KEY = "<YOUR API KEY>"

jina_embedding_model = JinaEmbedding(
    api_key=jina_ai_api_key,
    model="jina-embeddings-v2-base-en",
    encoding_queries='binary',
    encoding_documents='float'
)

jina_embedding_model.get_query_embedding('Query text here')
jina_embedding_model.get_text_embedding_batch(['X', 'Y', 'Z'])

tagAutres bases de données vectorielles prenant en charge les embeddings binaires

Les bases de données vectorielles suivantes fournissent une prise en charge native des vecteurs binaires :

tagExemple

Pour vous montrer les embeddings binaires en action, nous avons pris une sélection de résumés de arXiv.org, et obtenu à la fois des vecteurs en virgule flottante 32 bits et binaires en utilisant jina-embeddings-v2-base-en. Nous les avons ensuite comparés aux embeddings pour une requête exemple : « 3D segmentation ».

Vous pouvez voir dans le tableau ci-dessous que les trois premiers résultats sont les mêmes et quatre des cinq premiers correspondent. L'utilisation de vecteurs binaires produit des correspondances presque identiques.

	Binary		32-bit Float
Rang	Distance Hamming	Texte correspondant	Cosinus	Texte correspondant
1	0.1862	SEGMENT3D: A Web-based Application for Collaboration...	0.2340	SEGMENT3D: A Web-based Application for Collaboration...
2	0.2148	Segmentation-by-Detection: A Cascade Network for...	0.2857	Segmentation-by-Detection: A Cascade Network for...
3	0.2174	Vox2Vox: 3D-GAN for Brain Tumour Segmentation...	0.2973	Vox2Vox: 3D-GAN for Brain Tumour Segmentation...
4	0.2318	DiNTS: Differentiable Neural Network Topology Search...	0.2983	Anisotropic Mesh Adaptation for Image Segmentation...
5	0.2331	Data-Driven Segmentation of Post-mortem Iris Image...	0.3019	DiNTS: Differentiable Neural Network Topology...