Gli embeddings sono diventati la pietra angolare di una varietà di applicazioni di AI ed elaborazione del linguaggio naturale, offrendo un modo per rappresentare i significati dei testi come vettori multidimensionali. Tuttavia, tra le dimensioni crescenti dei modelli e le quantità sempre maggiori di dati elaborati dai modelli AI, le esigenze computazionali e di archiviazione per gli embeddings tradizionali sono aumentate. Gli embeddings binari sono stati introdotti come alternativa compatta ed efficiente che mantiene prestazioni elevate riducendo drasticamente i requisiti di risorse.
Gli embeddings binari sono un modo per mitigare questi requisiti di risorse riducendo la dimensione dei vettori di embedding fino al 96% (96,875% nel caso di Jina Embeddings). Gli utenti possono sfruttare la potenza degli embeddings binari compatti nelle loro applicazioni AI con una perdita minima di accuratezza.
tagCosa Sono gli Embeddings Binari?
Gli embeddings binari sono una forma specializzata di rappresentazione dei dati in cui i tradizionali vettori in virgola mobile multidimensionali vengono trasformati in vettori binari. Questo non solo comprime gli embeddings ma mantiene anche quasi tutta l'integrità e l'utilità dei vettori. L'essenza di questa tecnica risiede nella sua capacità di mantenere la semantica e le distanze relazionali tra i punti dati anche dopo la conversione.
La magia dietro gli embeddings binari è la quantizzazione, un metodo che trasforma numeri ad alta precisione in numeri a precisione inferiore. Nella modellazione AI, questo spesso significa convertire i numeri in virgola mobile a 32 bit negli embeddings in rappresentazioni con meno bit, come interi a 8 bit.

Gli embeddings binari portano questo all'estremo, riducendo ogni valore a 0 o 1. Trasformare numeri in virgola mobile a 32 bit in cifre binarie riduce la dimensione dei vettori di embedding di 32 volte, una riduzione del 96,875%. Le operazioni vettoriali sugli embeddings risultanti sono molto più veloci di conseguenza. Utilizzando le accelerazioni hardware disponibili su alcuni microchip si può aumentare la velocità dei confronti vettoriali di molto più di 32 volte quando i vettori sono binarizzati.
Alcune informazioni vengono inevitabilmente perse durante questo processo, ma questa perdita è minimizzata quando il modello è molto performante. Se gli embeddings non quantizzati di cose diverse sono massimamente differenti, allora è più probabile che la binarizzazione preservi bene quella differenza. Altrimenti, può essere difficile interpretare correttamente gli embeddings.
I modelli Jina Embeddings sono addestrati per essere molto robusti proprio in questo modo, rendendoli ben adatti alla binarizzazione.
Questi embeddings compatti rendono possibili nuove applicazioni AI, in particolare in contesti con risorse limitate come gli usi mobili e time-sensitive.
Questi benefici in termini di costi e tempi di calcolo comportano un costo relativamente piccolo in termini di prestazioni, come mostra il grafico seguente.

Per jina-embeddings-v2-base-en, la quantizzazione binaria riduce l'accuratezza di recupero dal 47,13% al 42,05%, una perdita di circa il 10%. Per jina-embeddings-v2-base-de, questa perdita è solo del 4%, dal 44,39% al 42,65%.
I modelli Jina Embeddings funzionano così bene quando producono vettori binari perché sono addestrati per creare una distribuzione più uniforme degli embeddings. Questo significa che due embeddings diversi saranno probabilmente più distanti l'uno dall'altro in più dimensioni rispetto agli embeddings di altri modelli. Questa proprietà assicura che quelle distanze siano meglio rappresentate dalle loro forme binarie.
tagCome Funzionano gli Embeddings Binari?
Per vedere come funziona, consideriamo tre embeddings: A, B e C. Questi tre sono tutti vettori in virgola mobile completi, non binarizzati. Ora, supponiamo che la distanza da A a B sia maggiore della distanza da B a C. Con gli embeddings, tipicamente usiamo la distanza del coseno, quindi:
Se binarizziamo A, B e C, possiamo misurare la distanza più efficientemente con la distanza di Hamming.
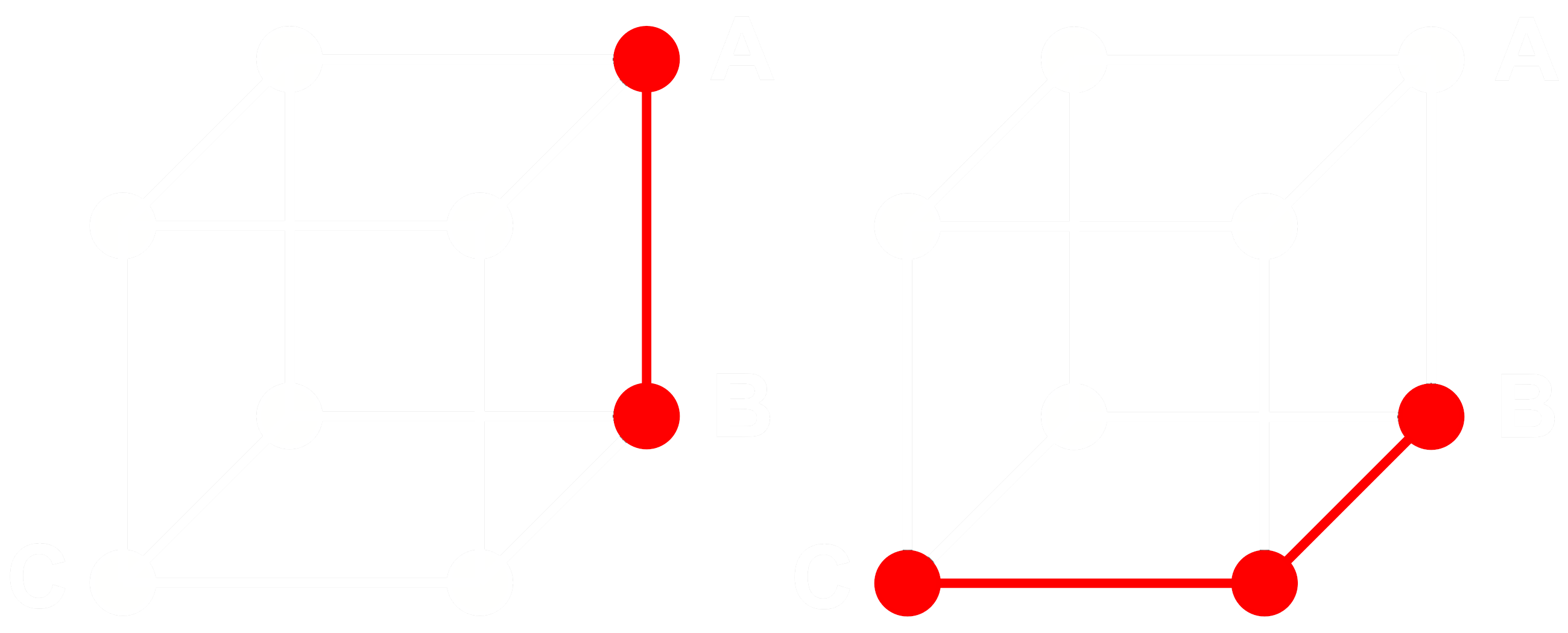
Chiamiamo Abin, Bbin e Cbin le versioni binarizzate di A, B e C.
Per i vettori binari, se la distanza del coseno tra Abin e Bbin è maggiore di quella tra Bbin e Cbin, allora la distanza di Hamming tra Abin e Bbin è maggiore o uguale alla distanza di Hamming tra Bbin e Cbin.
Quindi se:
allora per le distanze di Hamming:
Idealmente, quando binarizziamo gli embeddings, vogliamo che le stesse relazioni con gli embeddings completi valgano per gli embeddings binari come per quelli completi. Questo significa che se una distanza è maggiore di un'altra per il coseno in virgola mobile, dovrebbe essere maggiore per la distanza di Hamming tra i loro equivalenti binarizzati:
Non possiamo rendere questo vero per tutte le triplette di embeddings, ma possiamo renderlo vero per quasi tutte.
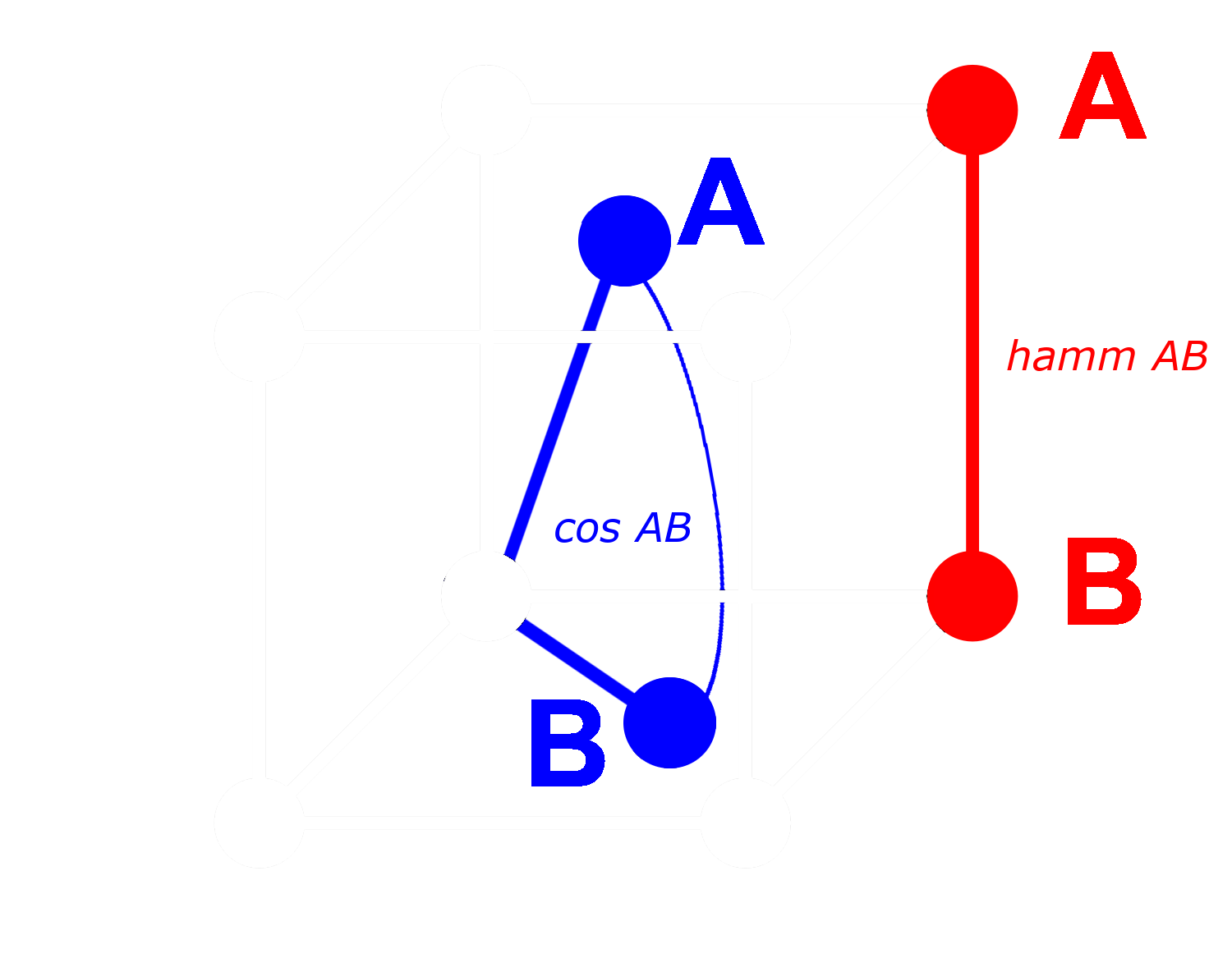
Con un vettore binario, possiamo trattare ogni dimensione come presente (uno) o assente (zero). Più distanti sono due vettori l'uno dall'altro in forma non binaria, maggiore è la probabilità che in una qualsiasi dimensione, uno abbia un valore positivo e l'altro un valore negativo. Questo significa che in forma binaria, ci saranno molto probabilmente più dimensioni dove uno ha uno zero e l'altro un uno. Questo li rende più distanti secondo la distanza di Hamming.
L'opposto si applica ai vettori che sono più vicini tra loro: Più vicini sono i vettori non binari, maggiore è la probabilità che in qualsiasi dimensione entrambi abbiano zeri o entrambi abbiano uno. Questo li rende più vicini secondo la distanza di Hamming.
I modelli Jina Embeddings sono così ben adatti alla binarizzazione perché li addestriamo usando il negative mining e altre pratiche di fine-tuning per aumentare particolarmente la distanza tra cose dissimili e ridurre la distanza tra quelle simili. Questo rende gli embeddings più robusti, più sensibili alle somiglianze e differenze, e rende la distanza di Hamming tra embeddings binari più proporzionale alla distanza del coseno tra quelli non binari.
tagQuanto Posso Risparmiare con gli Embeddings Binari di Jina AI?
Adottare i modelli di embedding binario di Jina AI non solo riduce la latenza nelle applicazioni time-sensitive, ma produce anche considerevoli benefici in termini di costi, come mostrato nella tabella seguente:
| Modello | Memoria per 250 milioni di embeddings |
Media del benchmark di recupero |
Prezzo stimato su AWS ($3.8 per GB/mese con istanze x2gb) |
|---|---|---|---|
| Embeddings in virgola mobile a 32 bit | 715 GB | 47.13 | $35,021 |
| Embeddings binari | 22.3 GB | 42.05 | $1,095 |
Questo risparmio di oltre il 95% è accompagnato da una riduzione di solo ~10% nell'accuratezza di recupero.
Questi risparmi sono ancora maggiori rispetto all'utilizzo di vettori binarizzati da OpenAI Ada 2 model o Cohere Embed v3, entrambi i quali producono embedding di output di 1024 dimensioni o più. Gli embedding di Jina AI hanno solo 768 dimensioni e mantengono prestazioni paragonabili ad altri modelli, rendendoli più piccoli anche prima della quantizzazione per la stessa accuratezza.
Questi risparmi sono anche ambientali, utilizzando meno materiali rari e meno energia.
tagPer Iniziare
Per ottenere embedding binari utilizzando la Jina Embeddings API, basta aggiungere il parametro encoding_type alla tua chiamata API, con il valore binary per ottenere l'embedding binarizzato codificato come interi con segno, o ubinary per interi senza segno.
tagAccesso Diretto alla Jina Embedding API
Usando curl:
curl https://api.jina.ai/v1/embeddings \
-H "Content-Type: application/json" \
-H "Authorization: Bearer <YOUR API KEY>" \
-d '{
"input": ["Your text string goes here", "You can send multiple texts"],
"model": "jina-embeddings-v2-base-en",
"encoding_type": "binary"
}'
O tramite l'API Python requests:
import requests
headers = {
"Content-Type": "application/json",
"Authorization": "Bearer <YOUR API KEY>"
}
data = {
"input": ["Your text string goes here", "You can send multiple texts"],
"model": "jina-embeddings-v2-base-en",
"encoding_type": "binary",
}
response = requests.post(
"https://api.jina.ai/v1/embeddings",
headers=headers,
json=data,
)
Con la richiesta Python sopra, otterrai la seguente risposta ispezionando response.json():
{
"model": "jina-embeddings-v2-base-en",
"object": "list",
"usage": {
"total_tokens": 14,
"prompt_tokens": 14
},
"data": [
{
"object": "embedding",
"index": 0,
"embedding": [
-0.14528547,
-1.0152762,
...
]
},
{
"object": "embedding",
"index": 1,
"embedding": [
-0.109809875,
-0.76077706,
...
]
}
]
}
Questi sono due vettori di embedding binari memorizzati come 96 interi a 8 bit con segno. Per decomprimerli in 768 0 e 1, devi utilizzare la libreria numpy:
import numpy as np
# assign the first vector to embedding0
embedding0 = response.json()['data'][0]['embedding']
# convert embedding0 to a numpy array of unsigned 8-bit ints
uint8_embedding = np.array(embedding0).astype(numpy.uint8)
# unpack to binary
np.unpackbits(uint8_embedding)
Il risultato è un vettore di 768 dimensioni con solo 0 e 1:
array([0, 0, 1, 1, 0, 1, 1, 0, 1, 1, 0, 0, 0, 1, 0, 1, 1, 1, 1, 1, 0, 0,
0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 1, 1, 0, 0, 0, 1, 1, 1, 0, 1, 0, 1,
0, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 1, 1, 0, 0, 0, 0, 1, 0, 1, 1, 1,
0, 0, 0, 0, 1, 1, 1, 0, 0, 1, 0, 0, 0, 0, 1, 1, 1, 1, 0, 1, 0, 1,
1, 1, 0, 1, 1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 0, 0, 0,
0, 0, 1, 0, 0, 0, 1, 0, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1, 0, 0, 1, 0,
1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 1,
1, 0, 1, 0, 1, 1, 0, 0, 0, 1, 0, 1, 1, 1, 0, 0, 1, 1, 0, 0, 0, 1,
1, 1, 0, 1, 0, 1, 1, 1, 1, 0, 1, 0, 0, 1, 0, 0, 1, 0, 1, 0, 1, 1,
0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 1, 1, 0, 1, 0, 0, 0, 1, 1, 1,
1, 0, 0, 1, 0, 0, 0, 1, 0, 1, 0, 0, 1, 0, 1, 0, 1, 0, 0, 1, 0, 0,
0, 0, 0, 0, 1, 0, 0, 0, 1, 1, 1, 0, 1, 1, 0, 1, 1, 0, 1, 0, 0, 0,
1, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1, 1, 0, 1, 1, 0, 0, 0, 1, 0, 0, 1,
0, 0, 0, 0, 0, 1, 1, 0, 0, 1, 1, 1, 1, 0, 1, 0, 1, 0, 1, 1, 1, 1,
1, 0, 1, 0, 0, 0, 1, 0, 0, 1, 0, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 0,
0, 0, 0, 0, 1, 0, 1, 1, 1, 0, 1, 1, 1, 1, 0, 0, 0, 0, 0, 1, 1, 1,
1, 1, 1, 1, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 1, 0, 1, 0, 1,
1, 0, 1, 1, 1, 0, 0, 1, 0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 0, 0, 1, 1,
0, 0, 0, 1, 1, 1, 1, 1, 0, 1, 1, 0, 1, 0, 0, 0, 1, 1, 0, 1, 1, 0,
1, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 1, 1, 1, 0, 1, 1, 1, 0,
0, 0, 0, 0, 0, 1, 1, 1, 1, 0, 1, 0, 1, 1, 0, 1, 0, 1, 1, 1, 0, 0,
0, 0, 1, 1, 1, 0, 1, 0, 1, 0, 0, 1, 0, 1, 0, 0, 0, 1, 1, 1, 0, 1,
0, 1, 1, 1, 0, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 0, 0, 1, 0,
0, 1, 1, 1, 0, 1, 1, 0, 0, 1, 1, 0, 1, 1, 0, 1, 1, 1, 0, 1, 1, 0,
1, 1, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 1, 1, 1, 0, 1, 1, 0,
0, 1, 0, 0, 1, 1, 0, 1, 0, 0, 1, 0, 0, 1, 0, 1, 0, 1, 1, 1, 0, 0,
0, 0, 1, 1, 0, 1, 0, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 0, 1,
1, 0, 1, 1, 0, 1, 1, 0, 1, 0, 0, 1, 0, 0, 0, 1, 0, 1, 0, 1, 1, 0,
1, 1, 1, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1, 0, 0, 1, 0, 1, 1, 0, 0,
1, 0, 1, 1, 1, 1, 1, 1, 1, 0, 1, 0, 0, 0, 1, 0, 0, 1, 1, 1, 0, 1,
1, 1, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 1, 1, 0, 1, 1, 0, 0, 1, 1, 0,
1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 1, 0, 0, 1, 1, 0, 1,
1, 1, 1, 0, 0, 1, 1, 1, 0, 1, 0, 0, 1, 1, 0, 1, 1, 1, 1, 1, 1, 0,
1, 1, 1, 0, 0, 1, 1, 0, 0, 1, 0, 0, 1, 1, 0, 0, 0, 1, 0, 1, 1, 1,
0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 0, 1, 0, 0],
dtype=uint8)
tagUtilizzo della Quantizzazione Binaria in Qdrant
Puoi anche utilizzare la libreria di integrazione di Qdrant per inserire direttamente gli embedding binari nel tuo vector store Qdrant. Poiché Qdrant ha implementato internamente BinaryQuantization, puoi utilizzarlo come configurazione preimpostata per l'intera collezione di vettori, consentendogli di recuperare e memorizzare vettori binari senza altre modifiche al tuo codice.
Vedi il codice di esempio qui sotto per come fare:
import qdrant_client
import requests
from qdrant_client.models import Distance, VectorParams, Batch, BinaryQuantization, BinaryQuantizationConfig
# Fornisci la chiave API di Jina e scegli uno dei modelli disponibili.
# Puoi ottenere una chiave di prova gratuita qui: https://jina.ai/embeddings/
JINA_API_KEY = "jina_xxx"
MODEL = "jina-embeddings-v2-base-en" # o "jina-embeddings-v2-base-en"
EMBEDDING_SIZE = 768 # 512 per la variante small
# Ottieni gli embedding dall'API
url = "https://api.jina.ai/v1/embeddings"
headers = {
"Content-Type": "application/json",
"Authorization": f"Bearer {JINA_API_KEY}",
}
text_to_encode = ["Il tuo testo va qui", "Puoi inviare testi multipli"]
data = {
"input": text_to_encode,
"model": MODEL,
}
response = requests.post(url, headers=headers, json=data)
embeddings = [d["embedding"] for d in response.json()["data"]]
# Indicizza gli embedding in Qdrant
client = qdrant_client.QdrantClient(":memory:")
client.create_collection(
collection_name="MyCollection",
vectors_config=VectorParams(size=EMBEDDING_SIZE, distance=Distance.DOT, on_disk=True),
quantization_config=BinaryQuantization(binary=BinaryQuantizationConfig(always_ram=True)),
)
client.upload_collection(
collection_name="MyCollection",
ids=list(range(len(embeddings))),
vectors=embeddings,
payload=[
{"text": x} for x in text_to_encode
],
)Per configurare la ricerca, dovresti utilizzare i parametri oversampling e rescore:
from qdrant_client.models import SearchParams, QuantizationSearchParams
results = client.search(
collection_name="MyCollection",
query_vector=embeddings[0],
search_params=SearchParams(
quantization=QuantizationSearchParams(
ignore=False,
rescore=True,
oversampling=2.0,
)
)
)tagUtilizzo di LlamaIndex
Per utilizzare gli embedding binari di Jina con LlamaIndex, imposta il parametro encoding_queries su binary quando istanzi l'oggetto JinaEmbedding:
from llama_index.embeddings.jinaai import JinaEmbedding
# Puoi ottenere una chiave di prova gratuita da https://jina.ai/embeddings/
JINA_API_KEY = "<LA TUA CHIAVE API>"
jina_embedding_model = JinaEmbedding(
api_key=jina_ai_api_key,
model="jina-embeddings-v2-base-en",
encoding_queries='binary',
encoding_documents='float'
)
jina_embedding_model.get_query_embedding('Testo della query qui')
jina_embedding_model.get_text_embedding_batch(['X', 'Y', 'Z'])
tagAltri Database Vettoriali che Supportano gli Embedding Binari
I seguenti database vettoriali forniscono supporto nativo per i vettori binari:
tagEsempio
Per mostrarti gli embedding binari in azione, abbiamo preso una selezione di abstract da arXiv.org, e abbiamo ottenuto sia vettori a virgola mobile a 32 bit che vettori binari utilizzando jina-embeddings-v2-base-en. Li abbiamo poi confrontati con gli embedding per una query di esempio: "3D segmentation".
Come puoi vedere dalla tabella seguente, le prime tre risposte sono le stesse e quattro delle prime cinque corrispondono. L'utilizzo di vettori binari produce corrispondenze quasi identiche.
| Binary | 32-bit Float | |||
|---|---|---|---|---|
| Rank | Hamming dist. |
Matching Text | Cosine | Matching text |
| 1 | 0.1862 | SEGMENT3D: A Web-based Application for Collaboration... |
0.2340 | SEGMENT3D: A Web-based Application for Collaboration... |
| 2 | 0.2148 | Segmentation-by-Detection: A Cascade Network for... |
0.2857 | Segmentation-by-Detection: A Cascade Network for... |
| 3 | 0.2174 | Vox2Vox: 3D-GAN for Brain Tumour Segmentation... |
0.2973 | Vox2Vox: 3D-GAN for Brain Tumour Segmentation... |
| 4 | 0.2318 | DiNTS: Differentiable Neural Network Topology Search... |
0.2983 | Anisotropic Mesh Adaptation for Image Segmentation... |
| 5 | 0.2331 | Data-Driven Segmentation of Post-mortem Iris Image... |
0.3019 | DiNTS: Differentiable Neural Network Topology... |