I modelli di Embedding/Reranking sono in grado di confrontare i numeri?

Questa è una domanda che mi è stata posta oggi alla conferenza ICML a Vienna.

Durante la pausa caffè, un utente di Jina mi ha avvicinato con una domanda nata da recenti discussioni nella comunità LLM. Mi ha chiesto se il nostro modello di embedding potesse riconoscere che 9.11 è più piccolo di 9.9, un compito in cui molti LLM forniscono il risultato opposto.

"Onestamente, non lo so", ho risposto. Mentre spiegava l'importanza di questa capacità per la sua applicazione e suggeriva che la tokenizzazione potrebbe essere la causa del problema, mi sono trovato ad annuire - la mia mente stava già elaborando idee per un esperimento per scoprire la risposta.

In questo articolo, voglio testare se il nostro modello di embedding, jina-embeddings-v2-base-en (rilasciato a ottobre 2023), e il Reranker, jina-reranker-v2-multilingual (rilasciato a giugno 2024), possono confrontare accuratamente i numeri. Per estendere l'ambito oltre il semplice confronto tra 9.11 e 9.9, ho progettato una serie di esperimenti che includono vari tipi di numeri: piccoli interi, numeri grandi, decimali, numeri negativi, valute, date e orari. L'obiettivo è valutare l'efficacia dei nostri modelli nel gestire diversi formati numerici.

tagSetup Sperimentale

L'implementazione completa può essere trovata nel Colab qui sotto:

Il design dell'esperimento è abbastanza semplice. Per esempio, per verificare se il modello di embedding comprende i numeri tra [1, 100]. I passaggi sono i seguenti:

Costruire i Documenti: Generare documenti con "stringhe letterali" per ogni numero da 1 a 100.
Inviare all'API di Embedding: Utilizzare l'API di Embedding per ottenere gli embedding per ogni documento.
Calcolare la Similarità del Coseno: Calcolare la similarità del coseno a coppie per ogni coppia di documenti per creare una matrice di similarità.
Creare lo Scatter Plot: Visualizzare i risultati utilizzando uno scatter plot. Ogni elemento $(i, j)$ nella matrice di similarità è mappato in un punto con: Asse X: $(i - j)$ ; Asse Y: il valore di similarità di $(i, j)$

Se il delta $(i - j)$ è zero, cioè $i = j$ , allora la similarità semantica dovrebbe essere massima. Man mano che il delta $(i - j)$ aumenta, la similarità dovrebbe diminuire. Idealmente, la similarità dovrebbe essere linearmente proporzionale al valore delta. Se non possiamo osservare tale linearità, è probabile che il modello non riesca a comprendere i numeri e possa produrre errori come dire che 9.11 è maggiore di 9.9.

Il modello Reranker segue una procedura simile. La differenza principale è che iteriamo attraverso i documenti costruiti, impostando ciascuno come query aggiungendo il prompt "what is the closest item to..." e classificando tutti gli altri come documents. Il punteggio di rilevanza restituito da l'API del Reranker viene utilizzato direttamente come misura di similarità semantica. L'implementazione principale è la seguente.

def rerank_documents(documents):
    reranker_url = "https://api.jina.ai/v1/rerank"
    headers = {
        "Content-Type": "application/json",
        "Authorization": f"Bearer {token}"
    }

    # Initialize similarity matrix
    similarity_matrix = np.zeros((len(documents), len(documents)))

    for idx, d in enumerate(documents):
        payload = {
            "model": "jina-reranker-v2-base-multilingual",
            "query": f"what is the closest item to {d}?",
            "top_n": len(documents),
            "documents": documents
        }
    ...

tagI Modelli Possono Confrontare Numeri tra [1, 2, 3, ..., 100]?

Scatter plot con media e varianza su ogni delta. Sinistra: jina-embeddings-v2-base-en; Destra: jina-reranker-v2-multilingual. documents = [str(i) for i in range(1, 101)]

tagCome Leggere Questi Grafici

Prima di procedere con altri esperimenti, permettetemi di spiegare come leggere correttamente questi grafici. Innanzitutto, la mia osservazione dai due grafici sopra è che il modello di embedding funziona bene, mentre il modello reranker non si comporta altrettanto bene. Quindi, cosa stiamo osservando e perché?

L'asse X rappresenta il delta degli indici $(i,j)$ , o $i-j$ , quando campioniamo uniformemente $d_i$ e $d_j$ dai nostri set di documenti. Questo delta varia da $[-100, 100]$ . Poiché il nostro set di documenti è ordinato per costruzione, cioè più piccolo è $|i-j|$ , più vicini sono semanticamente $d_i$ e $d_j$ ; più lontani sono $i$ e $j$ , minore è la similarità tra $d_i$ e $d_j$ . Ecco perché si vede la similarità (rappresentata dall'asse Y) raggiungere un picco a $X=0$ e poi diminuire linearmente spostandosi a sinistra e a destra.

Idealmente, questo dovrebbe creare un picco netto o una forma a "freccia verso l'alto" come ^. Tuttavia, non è sempre così. Se si fissa l'asse X in un punto, diciamo $X=25$ , e si guarda lungo l'asse Y, si trovano valori di similarità che vanno da 0.80 a 0.95. Ciò significa che $\mathrm{sim}(d_27, d_2)$ potrebbe essere 0.81 mentre $\mathrm{sim}(d_42, d_17)$ potrebbe essere 0.91 nonostante il loro delta sia sempre 25.

La linea di tendenza ciano mostra la similarità media per ogni valore X con la deviazione standard. Inoltre, notare che la similarità dovrebbe diminuire linearmente perché il nostro set di documenti è distribuito uniformemente, garantendo intervalli uguali tra documenti contigui.

Notare che i grafici di embedding saranno sempre simmetrici, con il valore Y massimo di 1.0 a $X=0$ Questo perché la similarità del coseno è simmetrica per $d_i$ e $d_j$ , e $\cos(0)=1$ .

D'altra parte, i grafici del reranker sono sempre asimmetrici a causa dei diversi ruoli della query e dei documenti nel modello reranker. Il valore massimo probabilmente non è 1.0 perché $X=0$ significa che usiamo il reranker per calcolare il punteggio di rilevanza di "what is the closest item to 4" vs "4". Se ci pensi, non c'è garanzia che $X=0$ porti al valore Y massimo.

tagI Modelli Possono Confrontare Numeri Negativi tra [-100, -99, -98, ..., -1]?

Scatter plot con media e varianza su ogni delta. Sinistra: jina-embeddings-v2-base-en; Destra: jina-reranker-v2-multilingual. Qui vogliamo testare se il modello può riconoscere la similarità semantica nello spazio negativo. documents = [str(-i) for i in range(1, 101)]

tagI Modelli Possono Confrontare Numeri con Intervalli Più Grandi [1000, 2000, 3000, ..., 100000]?

Qui vogliamo verificare se il modello può rilevare la similarità semantica quando confrontiamo numeri con un intervallo di 1000. documents = [str(i*1000) for i in range(1, 101)] Grafico a dispersione con media e varianza su ogni delta. Sinistra: jina-embeddings-v2-base-en; Destra: jina-reranker-v2-multilingual.

tagI Modelli Possono Confrontare Numeri da un Intervallo Arbitrario, es. [376, 377, 378, ..., 476]?

Qui vogliamo verificare se il modello può rilevare la similarità semantica quando confrontiamo numeri in un intervallo arbitrario, quindi spostiamo i numeri in un intervallo casuale documents = [str(i+375) for i in range(1, 101)] . Grafico a dispersione con media e varianza su ogni delta. Sinistra: jina-embeddings-v2-base-en; Destra: jina-reranker-v2-multilingual.

tagI Modelli Possono Confrontare Numeri Grandi tra [4294967296, 4294967297, 4294967298, ..., 4294967396]?

Qui vogliamo verificare se il modello può rilevare la similarità semantica quando confrontiamo numeri molto grandi. Seguendo l'idea dell'esperimento precedente, spostiamo l'intervallo ancora più in alto verso un numero grande. documents = [str(i+4294967296) for i in range(1, 101)] Grafico a dispersione con media e varianza su ogni delta. Sinistra: jina-embeddings-v2-base-en; Destra: jina-reranker-v2-multilingual.

tagI Modelli Possono Confrontare Numeri Decimali tra [0.0001, 0.0002, 0.0003, ...,0.1]? (senza cifre fisse)

Qui vogliamo verificare se il modello può rilevare la similarità semantica quando confrontiamo numeri decimali. documents = [str(i/1000) for i in range(1, 101)] Grafico a dispersione con media e varianza su ogni delta. Sinistra: jina-embeddings-v2-base-en; Destra: jina-reranker-v2-multilingual.

tagI Modelli Possono Confrontare Valute tra [ $1,$ 2, $3, ...,$ 100]?

Qui vogliamo verificare se il modello può rilevare la similarità semantica quando confrontiamo numeri in valuta. documents = ['$'+str(i) for i in range(1, 101)] Grafico a dispersione con media e varianza su ogni delta. Sinistra: jina-embeddings-v2-base-en; Destra: jina-reranker-v2-multilingual.

tagI Modelli Possono Confrontare Date tra [2024-07-24, 2024-07-25, 2024-07-26, ..., 2024-10-31]?

Qui vogliamo verificare se il modello può rilevare la similarità semantica quando confrontiamo numeri in formato data, cioè AAAA-MM-GG. today = datetime.today(); documents = [(today + timedelta(days=i)).strftime('%Y-%m-%d') for i in range(100)] Grafico a dispersione con media e varianza su ogni delta. Sinistra: jina-embeddings-v2-base-en; Destra: jina-reranker-v2-multilingual.

tagI Modelli Possono Confrontare Orari tra [19:00:07, 19:00:08, 19:00:09,..., 20:39:07]?

Qui vogliamo testare se il modello può riconoscere la similarità semantica quando confrontiamo numeri in formato orario, ovvero hh:mm:ss. now = datetime.now(); documents = [(now + timedelta(minutes=i)).strftime('%H:%M:%S') for i in range(100)] Grafico a dispersione con media e varianza su ogni delta. A sinistra: jina-embeddings-v2-base-en; A destra: jina-reranker-v2-multilingual.

tagOsservazioni

Ecco alcune osservazioni dai grafici sopra riportati:

tagModelli Reranker

I modelli reranker hanno difficoltà nel confrontare i numeri. Anche nel caso più semplice di confronto tra numeri nell'intervallo [1, 100], le loro prestazioni sono mediocri.
È importante notare la particolare costruzione del prompt utilizzata per le query nel nostro utilizzo del reranker, ovvero what is the closest item to x, poiché questo potrebbe influenzare i risultati.

tagModelli di Embedding

I modelli di embedding funzionano ragionevolmente bene quando confrontano piccoli numeri interi nell'intervallo [1, 100] o numeri negativi nell'intervallo [-100, 1]. Tuttavia, le loro prestazioni peggiorano significativamente quando si sposta questo intervallo ad altri valori, si aggiungono più intervalli o si trattano numeri decimali più grandi o più piccoli.
Si possono osservare picchi regolari a determinati intervalli, solitamente ogni 10 passi. Questo comportamento potrebbe essere legato al modo in cui il tokenizer elabora le stringhe, potenzialmente tokenizzando una stringa in "10" o "1" e "0".

tagComprensione di Date e Orari

Curiosamente, i modelli di embedding sembrano avere una buona comprensione di date e orari, confrontandoli correttamente nella maggior parte dei casi. Per i grafici delle date, i picchi appaiono ogni 30/31 passi, corrispondenti al numero di giorni in un mese. Per i grafici degli orari, i picchi appaiono ogni 60 passi, corrispondenti ai minuti in un'ora.
Anche i modelli reranker sembrano catturare questa comprensione in una certa misura.

tagVisualizzazione della Similarità con "Zero"

Aggiornato il 29 luglio 2024

Un altro esperimento interessante, probabilmente più intuitivo, è visualizzare direttamente il punteggio di similarità o rilevanza tra qualsiasi numero e lo zero (cioè l'origine). Fissando il punto di riferimento come l'embedding di zero, vogliamo vedere se la similarità semantica diminuisce linearmente man mano che i numeri diventano più grandi. Per il reranker, possiamo fissare la query a "0" o "What is the closest number to number zero?" e classificare tutti i numeri per vedere se i loro punteggi di rilevanza diminuiscono all'aumentare dei numeri. I risultati sono mostrati di seguito:

Qui, fissiamo l'"embedding di origine" all'embedding di "zero" e verifichiamo se la similarità semantica tra qualsiasi numero e zero è proporzionale al valore del numero. Specificamente, usiamo documents = [str(i) for i in range(2048)]. È mostrato il grafico a dispersione con media e varianza per ogni delta. A sinistra: jina-embeddings-v2-base-en; A destra: jina-reranker-v2-multilingual.

tagConclusione

Questo articolo illustra come i nostri attuali modelli di embedding e reranker gestiscono i confronti numerici. Nonostante la configurazione sperimentale relativamente semplice, espone alcuni difetti fondamentali nei modelli attuali e fornisce preziosi spunti per lo sviluppo del nostro prossimo embedding e reranker.

Due fattori chiave determinano se un modello può confrontare accuratamente i numeri:

Primo, la tokenizzazione: Se il vocabolario include solo le cifre 0-9, allora 11 potrebbe essere tokenizzato in token separati 1 e 1, o come un singolo token 11. Questa scelta influenza la comprensione dei valori numerici da parte del modello.

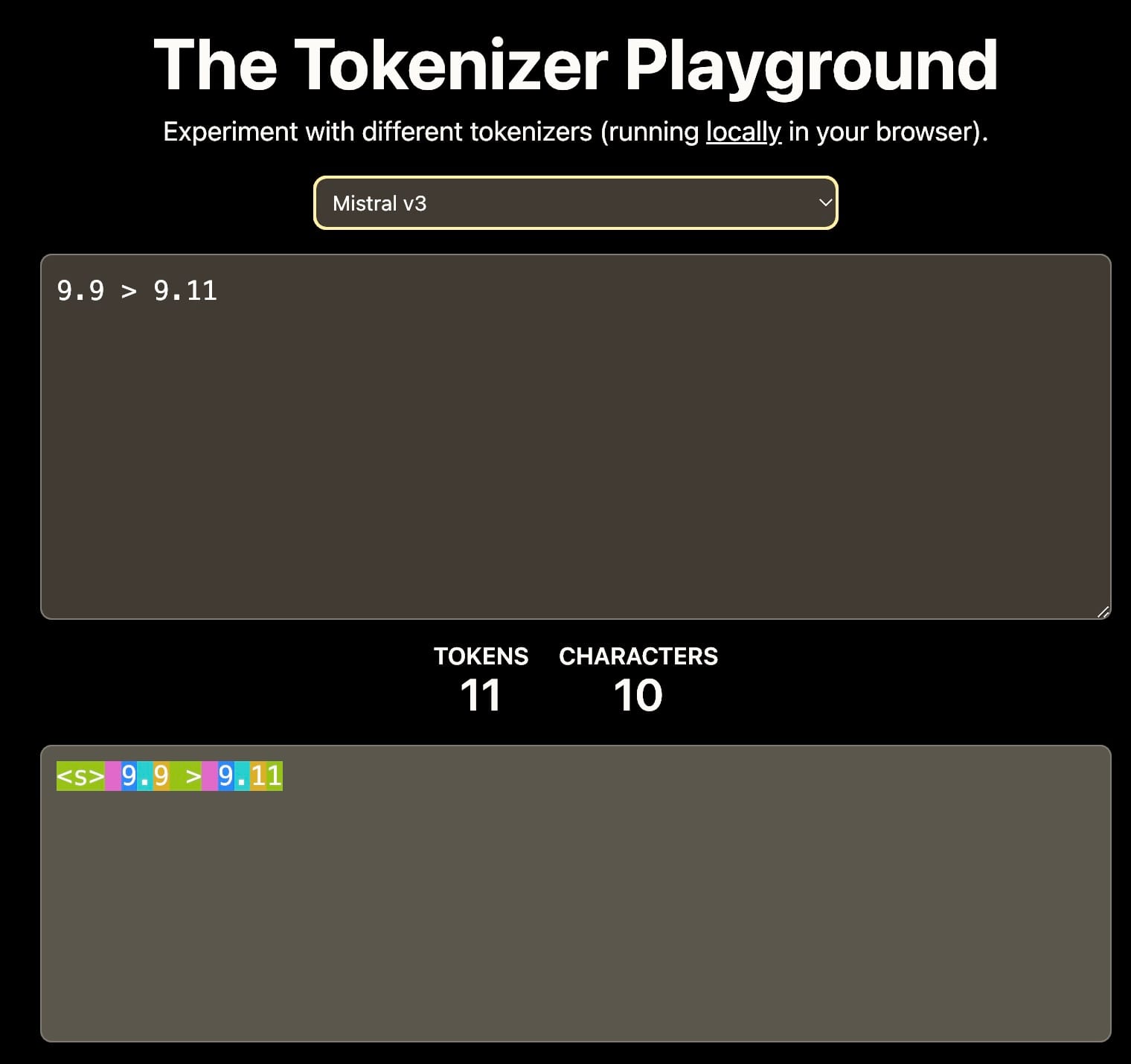
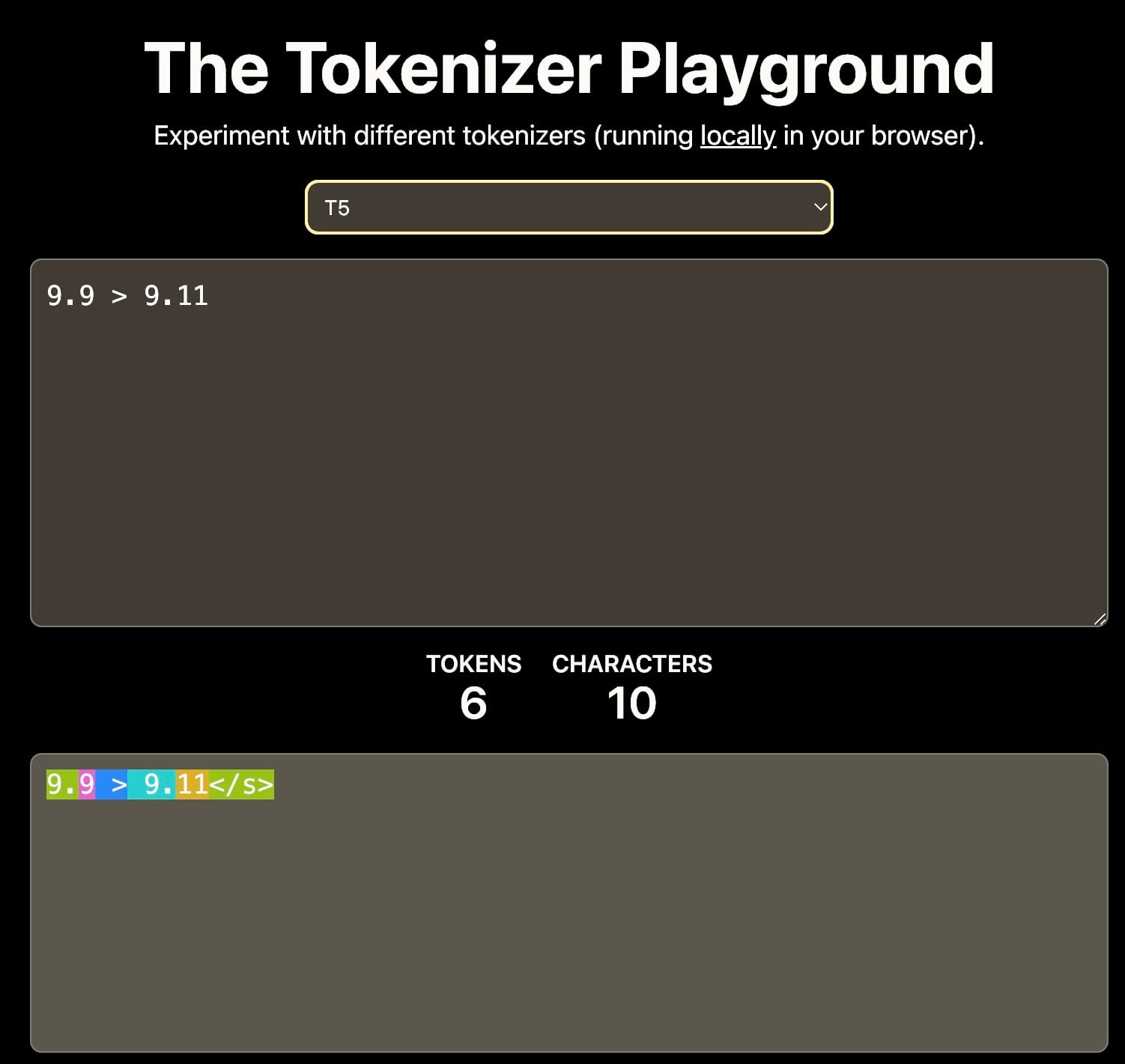
Tokenizer diversi portano a diverse interpretazioni di 9.11. Questo può influenzare l'apprendimento contestuale a valle. Fonte: The Tokenizer Playground su HuggingFace.

Secondo, i dati di training: Il corpus di training influenza significativamente le capacità di ragionamento numerico del modello. Ad esempio, se i dati di training includono principalmente documentazione software o repository GitHub dove il versionamento semantico è comune, il modello potrebbe interpretare che 9.11 è maggiore di 9.9, poiché 9.11 è la versione minore che segue 9.9.

La capacità aritmetica dei modelli di recupero denso, come gli embedding e i reranker, è cruciale per le attività che coinvolgono RAG e il recupero e ragionamento avanzato. Forti capacità di ragionamento numerico possono migliorare significativamente la qualità della ricerca, in particolare quando si tratta di dati strutturati come JSON.