Embeddings: The Swiss Army Knife of AI

A Swiss Army knife is a versatile, compact tool that you can keep in your pocket until you need it. It’s handy and designed to meet common unplanned needs. Have to cut something? It’s a knife. Have to unscrew something? It’s a screwdriver. Need to open a bottle or a can? It can do that, too. They’ve become so famous that “to be the Swiss Army knife of something” is now a figure of speech used for any versatile, adaptable, and highly useful tool.

AI tools are a bit too abstract to put in your pocket, but just because a tool is abstract doesn’t mean that words like specialized, versatile, and adaptable don’t apply to it!

One of AI's most versatile, adaptable, albeit abstract, tools goes by the name embeddings. Embeddings are actively in use for:

• Search and information retrieval for all media types
• Question-answering systems
• Recommender systems
• Outlier detection (often as part of fraud detection)
• Spellchecking and grammar correction
• Natural language understanding
• Machine translation

This is a far from exhaustive list. Nearly every AI application uses them. Even image generators and chatbots like ChatGPT rely on embeddings internally.

tagWhat is an embedding?

An embedding is a representation of some data object as a vector, constructed so that some properties of the data object are encoded into the geometric properties of its vector representation.

That’s awfully abstract, but it’s not really as complicated as it sounds.

First, we need to introduce a little (very little) bit of math. A vector is two things that sound like they're different but are actually the same:

1. A vector is a point in a multidimensional space.
2. A vector is an ordered list of scalar values, i.e., numbers.

To see how this works, consider lists of two numbers. For example, $(6, 4)$ and $(2, 8)$. You see that we could treat them as coordinates on an x-y axis, with each list corresponding to a point in a two-dimensional space:

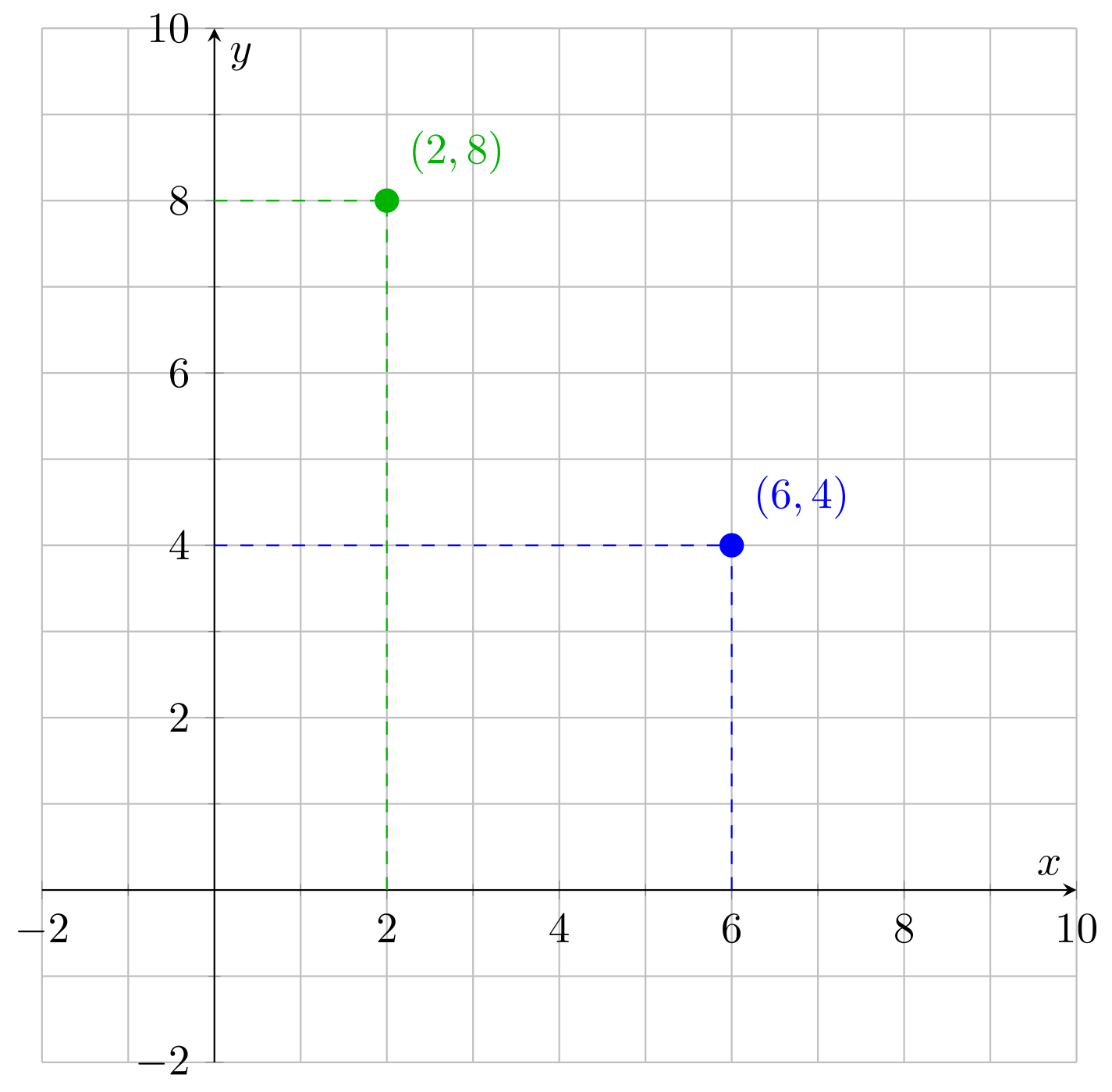
If we have three numbers, like $(3, 2, 5)$ and $(4, 5, 2)$, then this corresponds to points in a three-dimensional space:

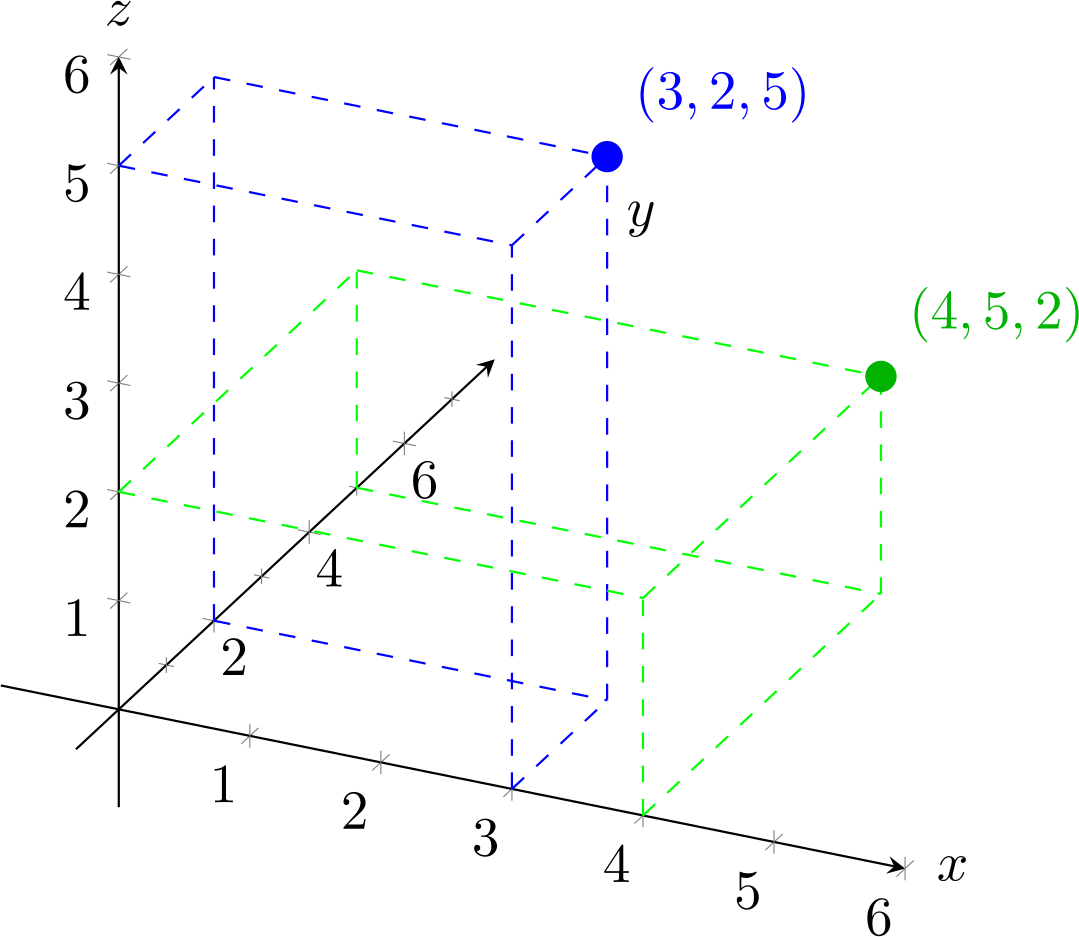
The important point is that we could extend this into more dimensions: four, five, a hundred, a thousand, even millions or billions. Drawing a space with a thousand dimensions is very hard, and imagining one is all but impossible, but mathematically, it’s really easy.

For example, the distance between points $(6, 4)$ and $(2, 8)$ is simply an application of Pythagoras’ theorem. Given two points $a = (x_1, y_1)$ and $b = (x_2, y_2)$, the distance between them is:

For $(6, 4)$ and $(2, 8)$, this means:

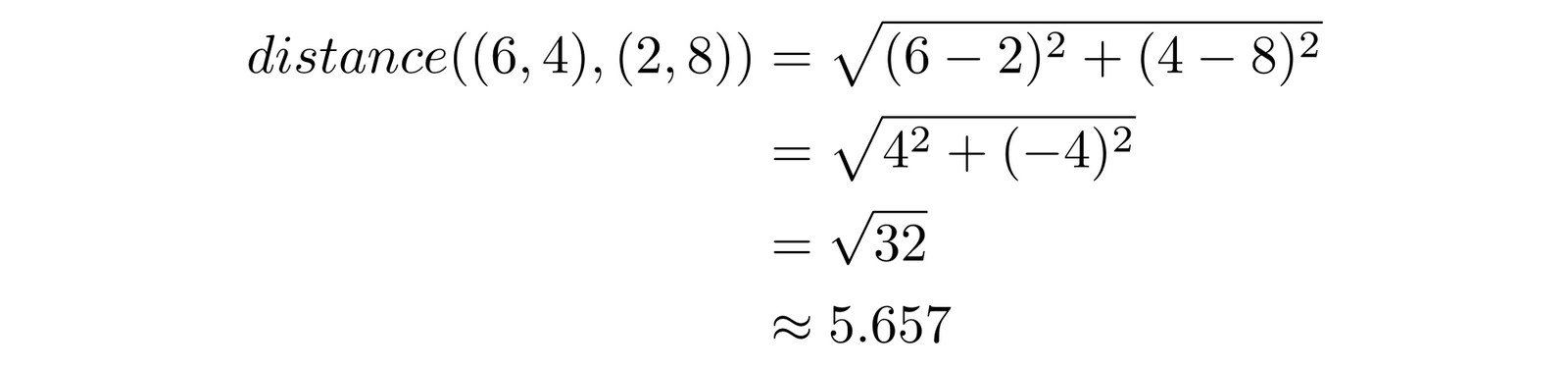
For three dimensions, we just extend the formula by adding a term. For $a = (3, 2, 5)$ and $b = (4, 5, 2)$:

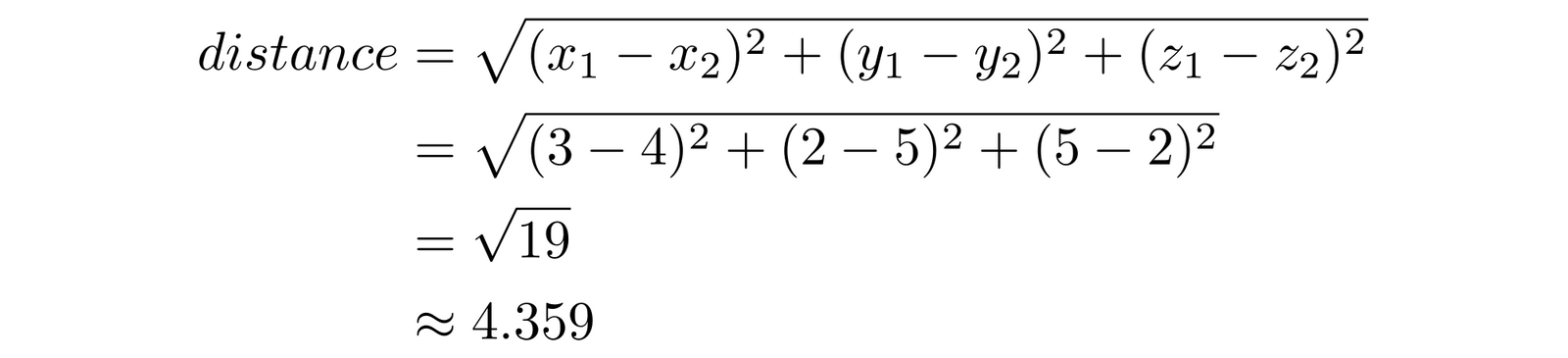
We can extend this formula to vectors in any number of dimensions. We just add more terms, the same way we did by going from two to three dimensions.

Besides distance, another measurement we use in high-dimensional vector spaces is the cosine of the angle between the two vectors. If you see each vector not just as a point but as a line from the origin (the point designated by the vector $(0,0,0,...)$), then you can calculate the angle between the two vectors ($\theta$ in the image below).

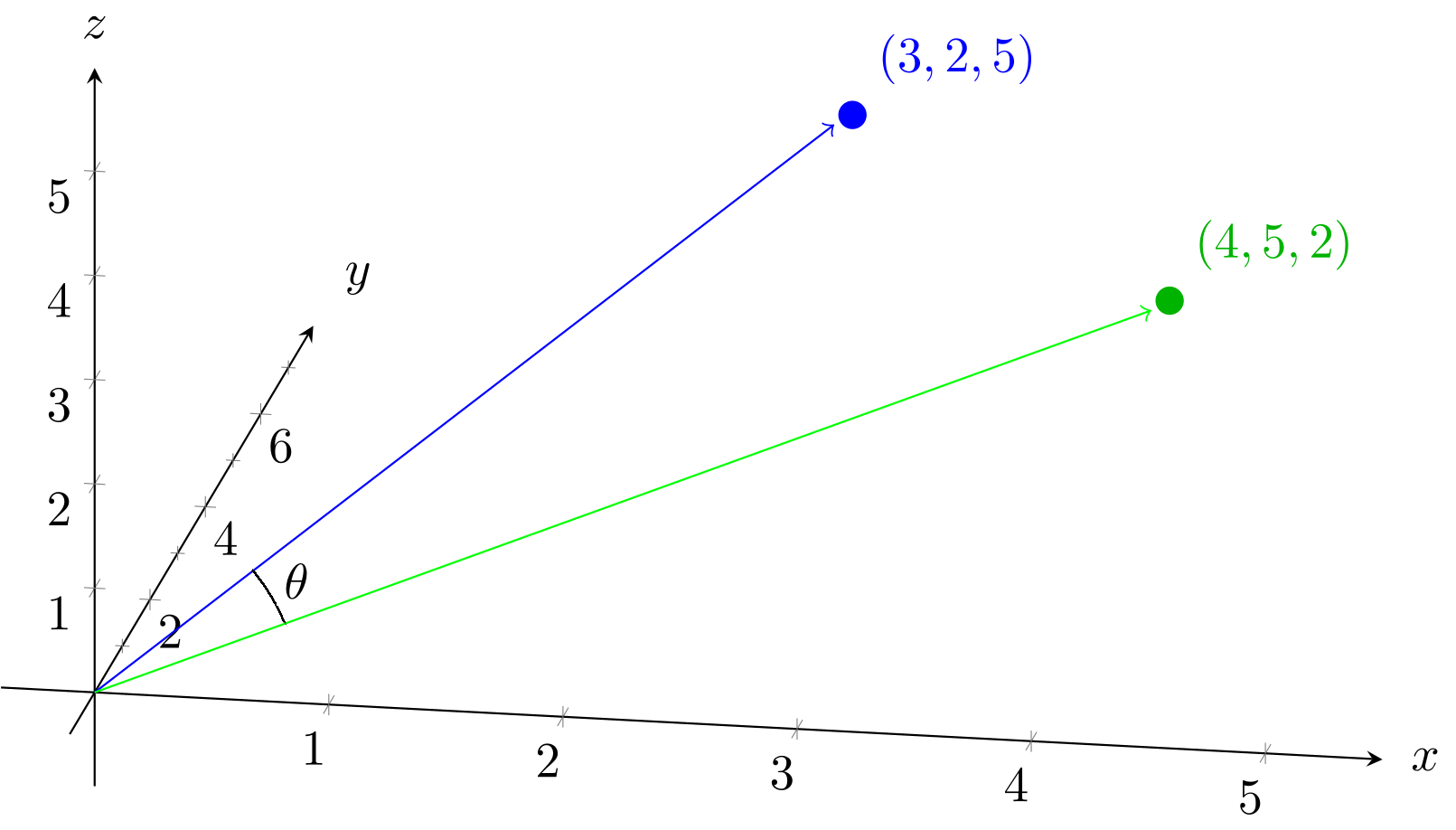
To calculate this, we have another formula that scales up to any number of dimensions. We know that the cosine of the angle $\theta$ between vectors $a$ and $b$ is:

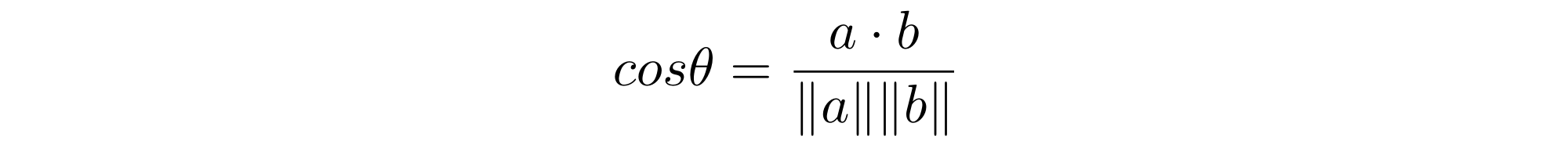
This is more complicated than it looks, but not much. $a \cdot b$ is called the dot product of the two vectors, and it’s easy to calculate. If $a = (3, 2, 5)$ and $b = (4, 5, 2)$, then:

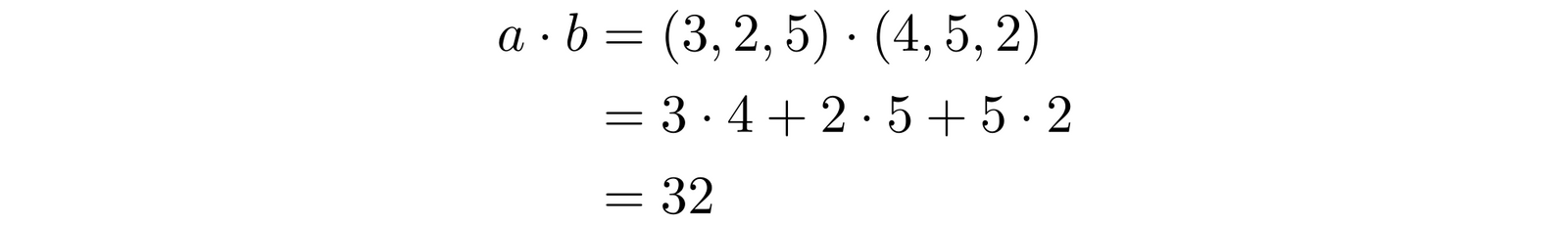
As for $‖a‖$ and $‖b‖$, those are the lengths of the vectors, i.e., the distance from the origin to that point. So:

Therefore, to calculate $cos \theta$:

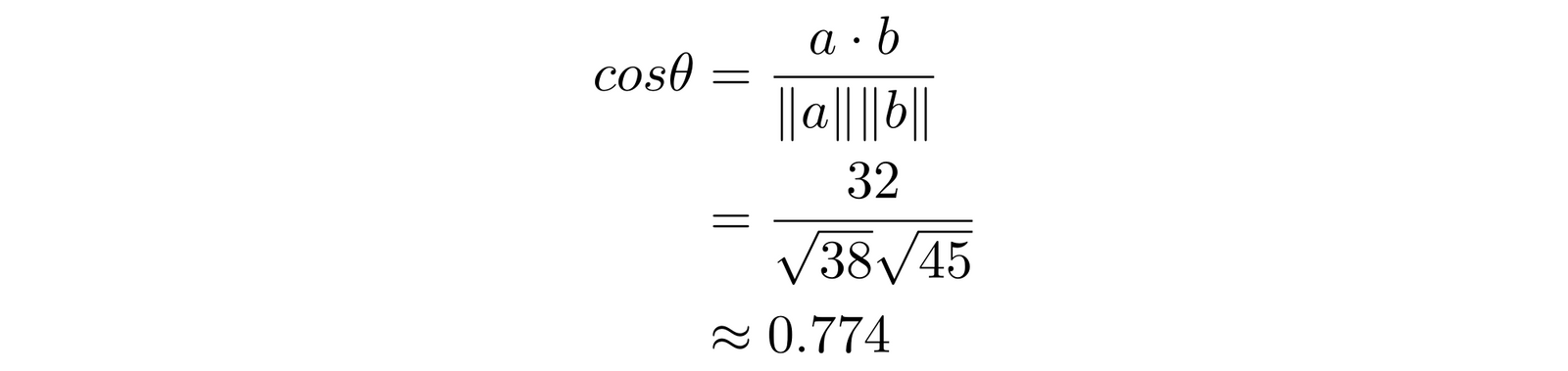
This cosine corresponds to an angle of approximately 39.3°, but in machine learning, we typically stop once we’ve calculated the cosine because if all the numbers in both vectors are greater than zero, then the cosine of the angle will be between 0 and 1.

This looks like a lot of math, but if you look it over, you’ll see that it’s just addition, subtraction, multiplication, division, one exponent, and a square root. Simple but boring and repetitive stuff. You don’t actually have to do any of this math. The whole reason we keep computers around is to do that sort of thing. But you should understand that vectors are lists of numbers, understand the concept of working with vectors, and understand how, no matter how many dimensions a vector has, we can still do things like calculate distances and angles.

What makes this so important is that any data we keep on a computer is also just a list of numbers. Every data item — digital pictures, texts, audio recordings, 3D model files, anything you can think of that you can put into a computer file — is a vector if we choose to look at it that way.

tagHow do we assign embedding vectors to things?

The point of embeddings is to assign vectors to data objects so that their placement in high-dimensional spaces encodes useful information about them. The data objects — texts or images or whatever else we’re working with — are already vectors if we choose to look at them that way. The locations of those vectors don’t tell us anything useful about them.

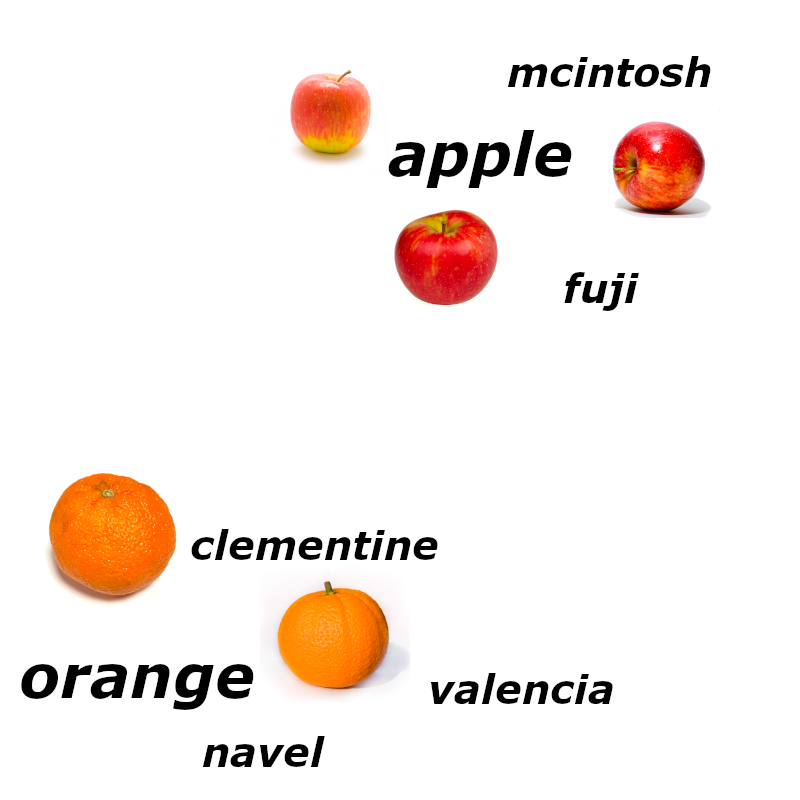
Consider these four images:

Each is a 450x450 pixel image colored with the standard RGB palette. This means the picture consists of 202,500 pixels, each with one number between 0 and 255 for its red, green, and blue values. To turn this into a vector with 607,500 dimensions is trivial.

We could take any pair of images and calculate the distance between them or measure their cosine, but it would be very unlikely that the apples would be especially close to each other or especially far from the oranges. At least, it would be very unlikely if we used hundreds of pictures of apples and oranges instead of just four.

More likely, we would get something like this:

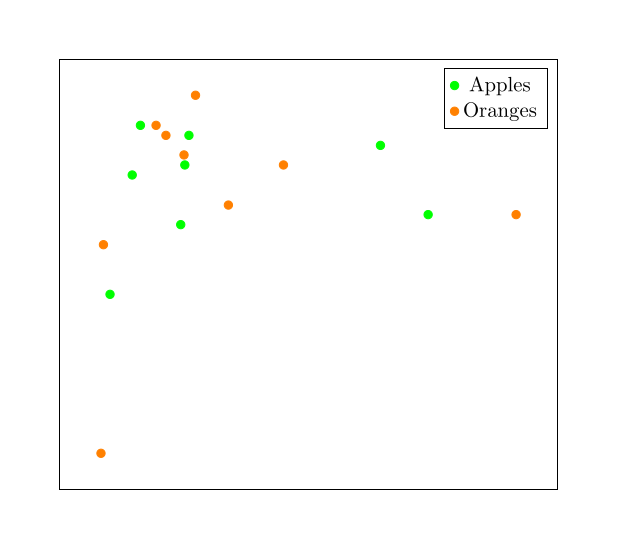
We can’t draw pictures in 600,000 dimensions, so this picture uses just two dimensions to demonstrate the point: We should expect that the apples and oranges are semi-randomly placed and mixed up together.

We want to assign to each image a unique embedding such that the apples are close together and far from the oranges, and vice-versa. We want something like this:

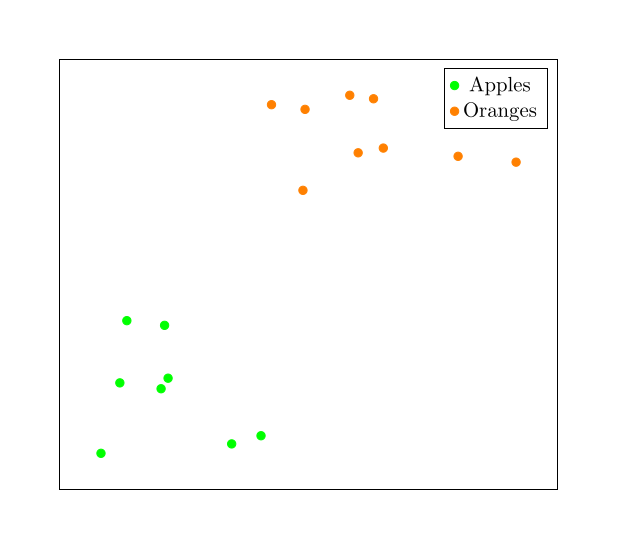
To do that, we construct a neural network (which we’re going to call an embedding model) that takes 607,500 dimension vectors as input and outputs some other vector, typically with fewer dimensions. For example, the widely used ViT-B-32 image embedding model transforms input images into 512-dimension embedding vectors.

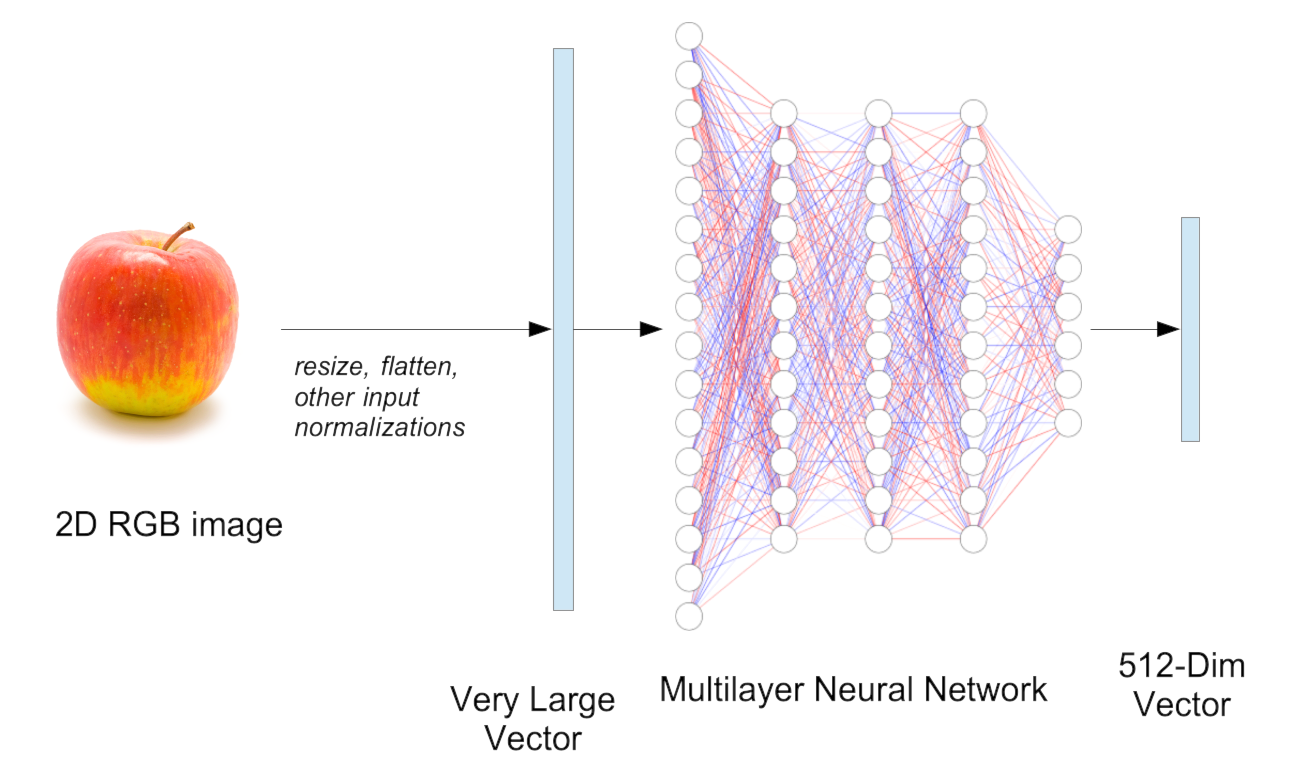
We then train the embedding model with labeled pictures of apples and oranges, instructing it to adjust the network’s weights slowly to separate the embedding vectors for apples and oranges. After many cycles of training, we expect that when we give the model pictures of apples as input, it will output vectors that are closer to each other than they are to the vectors we get when we give it pictures of oranges as inputs.

Those output vectors are embeddings, and they collectively form an embedding space. Individual embeddings’ locations encode useful information about their corresponding data objects: In this case, whether something is a picture of an apple or an orange.

Telling apples from oranges is a very simplistic scenario, but you might easily imagine scaling it up to many features.

In some use cases, we can even construct embeddings where we don’t explicitly say what features are relevant, and we let the neural network figure it out in the training process. For example, we can construct a face recognition system by taking pictures of people’s faces and training an embedding model to output embeddings that place pictures of the same person close together. We can then construct a database of people's pictures with their embedding vectors as keys.

We would expect the stored faces to be distributed through the embedding space:

We might expect that this embedding space would encode a lot of features that we had never explicitly trained it to encode. For example, it might segregate men from women:

Or we might find people clustered together by features of their hair, like baldness or grey:

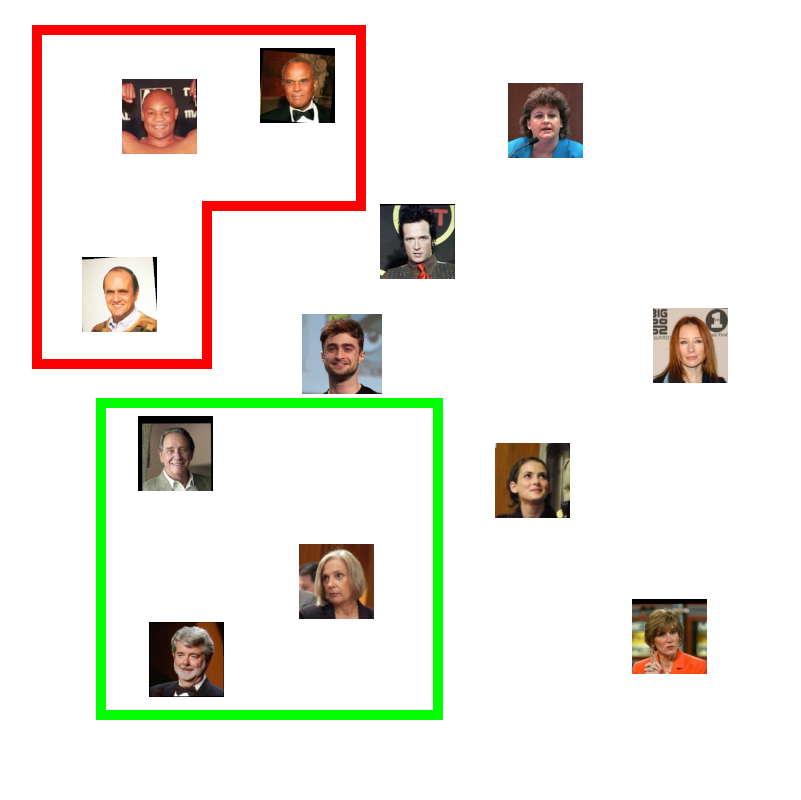
But we would expect that if we gave it another picture of someone in the database, the embedding for that new picture would be closer to the picture we stored of that person than to anyone else:

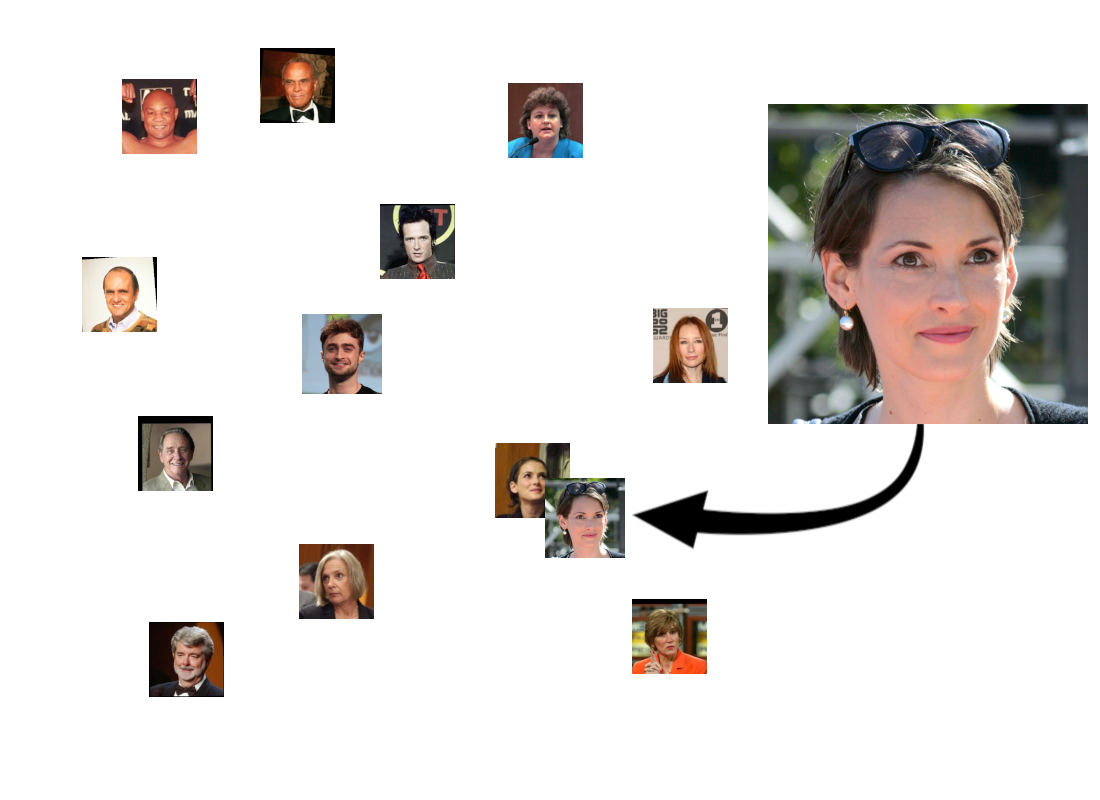
Of course, it would also find people who just look similar, although we hope that they wouldn’t be as close together as two people who are actually the same:

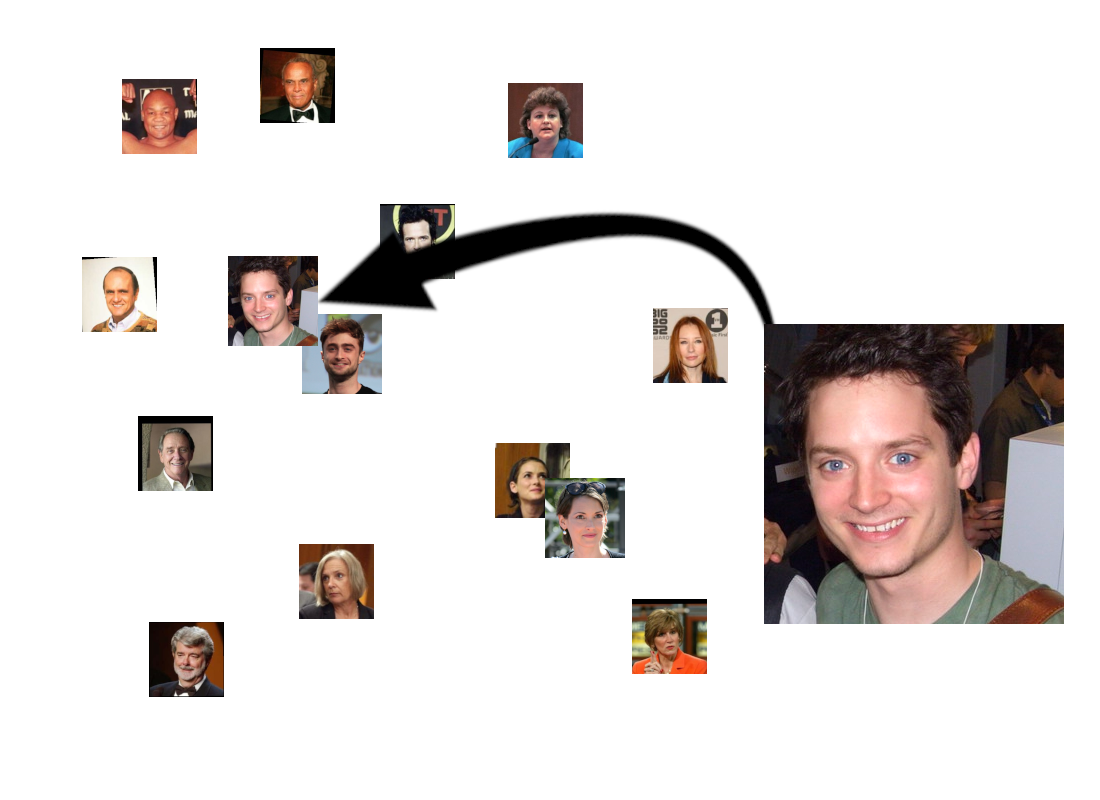
This highlights the logic of embedding spaces: Inputs are diverse, but by translating them into embeddings, we turn features — sometimes complex, hidden, subtle, or non-obvious features — into geometric properties that software can easily identify.

Embedding spaces can also support diverse input types, like text and images, creating a common embedding space and enabling you to map between the two.

For example, if we have a database of pictures with descriptive captions, we can co-train two embedding models — one for images and one for texts — to output vectors in the same embedding space. The result is that embeddings of descriptions of images and embeddings of the images themselves will be near each other.

In principle, any kind of digital data can serve as input for creating embeddings, and any paired data types — not just text and images — can serve to create multi-modal joint embedding spaces.

tagWhat are embeddings good for?

Like the Swiss Army knife, the question should be, what aren’t they good for?

We’ve already shown how you can use embeddings for image classification and face recognition, but that’s far from exhausting the possibilities. For example, AI image production from text descriptions (a.k.a. “AI art”) starts by constructing a joint embedding space for text and images, and then, when the user enters a text, it calculates that text’s embedding and tries to construct an image that will produce a nearby embedding.

Embeddings are so generally useful that they see applications all over AI and machine learning. Any application that requires similarity/dissimilarity evaluation, relies on hidden or non-obvious features, or requires implicit context-sensitive mappings between different inputs and outputs, likely uses embeddings in some form.

tagConclusion

Embeddings are an essential technology for modern machine learning and AI, present in some form across the spectrum of AI applications. Properly understanding and mastering this technology positions you to leverage AI models to add the most value to your business.

The theory behind embeddings isn’t even complicated: All it involves is a map from data objects to points in a high dimensional vector space where things that have properties in common that matter to you cluster together. Using them is just a matter of measuring vector distances and cosines, which is computationally trivial math!

Unfortunately, the practice of constructing and training embedding models is more complex than using them. Jina AI is developing a collection of high-performance specialized embedding models that you can download or use via our public API, without any of the complexities of AI development. We are also preparing a suite of open-source tools in Python to help you integrate embedding models into your tech stack.

Jina AI is committed to providing you with tools and help for creating, optimizing, evaluating, and implementing embedding models for your enterprise. We’re here to help you navigate the new world of business AI. Contact us via our website or join our community on Discord to get started.

Jina AI - Your Portal to Multimodal AI

Jina AI offers powerful multimodal AI solutions for everyday users, developers, and scalable enterprise solutions. We aim to democratize access to the limitless potential of AI-generated creativity and innovation, empowering individuals and businesses alike.

Your Portal to Multimodal AI

Join the Jina AI Discord Server!

Check out the Jina AI community on Discord - hang out with 2677 other members and enjoy free voice and text chat.

Discord