Embeddings are a core concept and technology in artificial intelligence, used in some form in practically all recent AI models, including ChatGPT and image generators like Stable Diffusion. It is one of the fundamental technologies behind the most visible and useful AI applications.
Embeddings are also important to less flashy applications, like search, visual face and object recognition, machine translation, recommenders, and many more.
An embedding is a vector that stands in for some other object (digital, physical, or abstract) such that some of the properties of the object it stands for are preserved as geometric properties of their corresponding vectors.
This post tries to explain what that means concretely.
tagVectors
A vector is just a list of numbers that we can interpret as coordinates in a high-dimensional space.
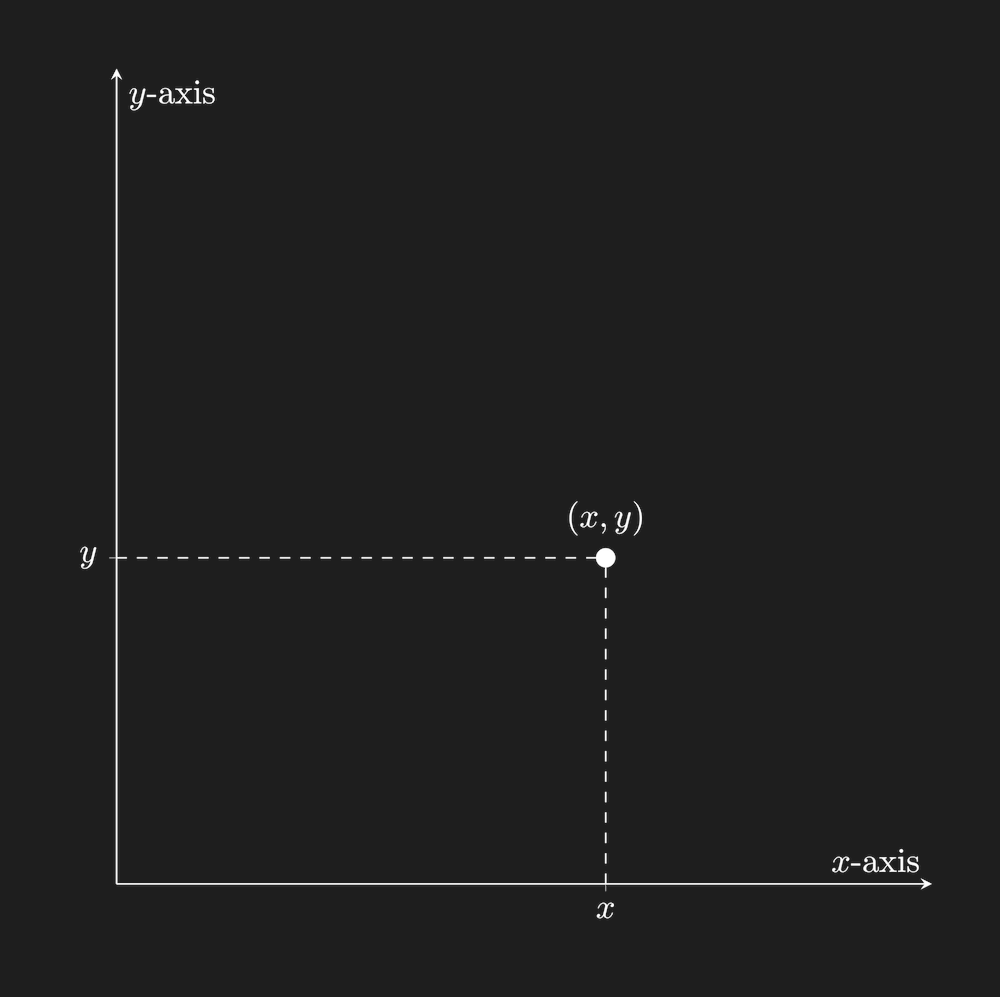
Imagine a list of two numbers . We could treat them as coordinates on an x-y graph, with each list corresponding to a point in a two-dimensional space:
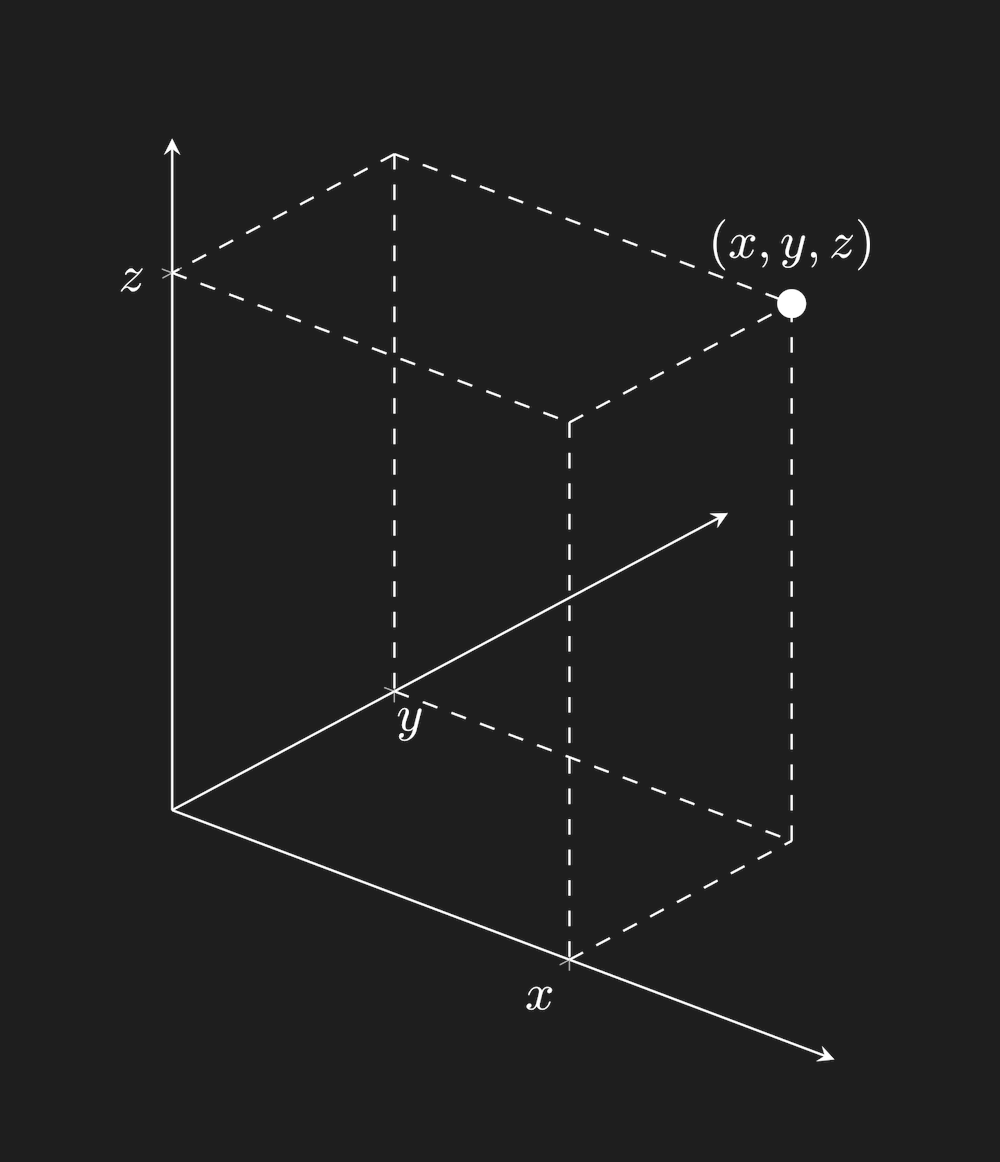
If we have three numbers , then this corresponds to a point in a three-dimensional space:
We can readily extend this logic into more dimensions: four, five, a hundred, a thousand, even millions or billions. Drawing a space with a thousand dimensions is very hard, and imagining one is all but impossible, but mathematically, it’s trivial to manage.
tagEmbeddings as Vectors
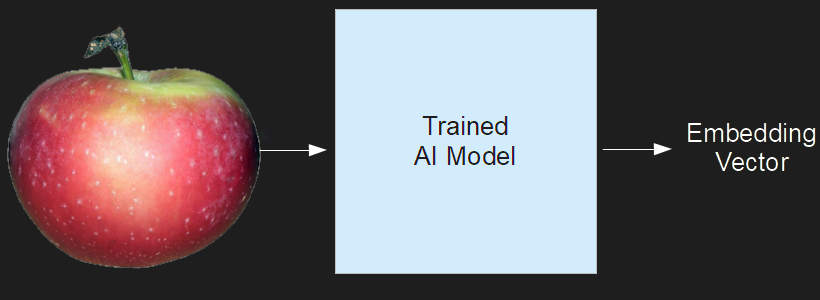
For example, let’s say we had a way to assign a small vector — just two numbers long — to pictures of apples and oranges.

We can display vectors of just two numbers as points on an XY graph, so imagine we took pictures of apples and oranges and assigned each a random vector, then plotted them on a graph:

The apples and oranges are all mixed together, and nothing about how they’re placed on the graph tells us whether a picture is of an apple or an orange.
What we’d like to have is something like this:
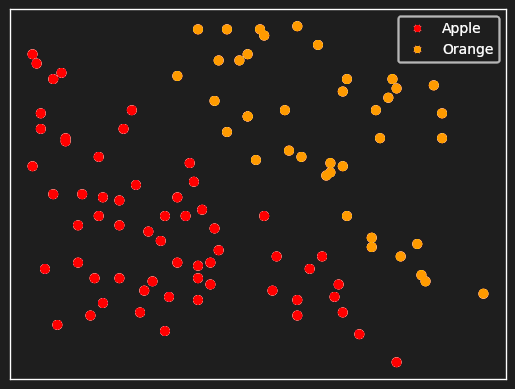
If we had the means to assign vectors like these to pictures of apples and oranges, it would be trivial to write a program to tell them apart. All it would have to do is check which side of a line the vector fell on.
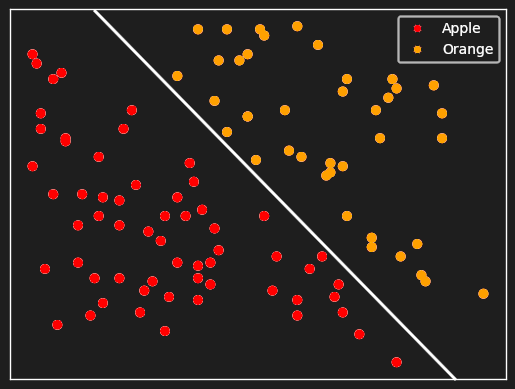
AI and neural networks provide a way to do exactly that.
Using machine learning, we can construct an AI model that takes images and then outputs vectors such that the oranges and apples are easily separated. These vectors typically have a lot more than two dimensions, so they aren’t easy to draw.
The property of the original object that we care about — whether it is an apple or an orange — is preserved in the geometry of the embedding vectors: The apples are all to one side and the oranges to the other, easily separated by what in high-dimensional geometry is called a hyper-plane, but is really just a simple way of splitting the embedding space.
This example is very simple and concerns only one distinction: apples or oranges. Embeddings can capture a lot of information about many different aspects of the objects they represent. If we trained an AI model to distinguish apples from oranges, we would likely find that the embeddings encoded many of the characteristics that distinguish apples from oranges, like color and texture and the presence of a stem. We might additionally find that the green apples are clustered together, farther from the red ones, or that highly mottled apples had embeddings closer to the oranges.
tagWord Embeddings
Embeddings emerge almost automatically from neural network-based AI models, as we will show in the next section, but they were first developed as a way to better encapsulate the semantics (i.e. meanings) of words for computers. You will still sometimes see people talk about "semantic embeddings" because of the role word embeddings have played in this technology, even though embeddings aren’t specifically about some kind of real-world meaning but about any useful property that an AI model can learn to recognize.
In natural language processing, embeddings have always been associated with an idea in linguistics called the distributional hypothesis, most frequently associated with the linguist J.R. Firth:
You shall know a word by the company it keeps.
A Synopsis of Linguistic Theory, 1930-55.
(In Studies in Linguistic Analysis, 1957, pp. 1-31)
The distributional hypothesis is the idea that the semantics — that is to say, the meaning — of a word is reflected in the contexts of its usage. We should expect that the more related the meanings of two words, the more we should see them in the same contexts.
For example, when two words are spelled or pronounced the same, we use context to figure out which word is intended:
- She took her bat to baseball practice.
- She was chased away from the cave by a bat.
It is clear from the surrounding context which meaning of the word bat is intended.

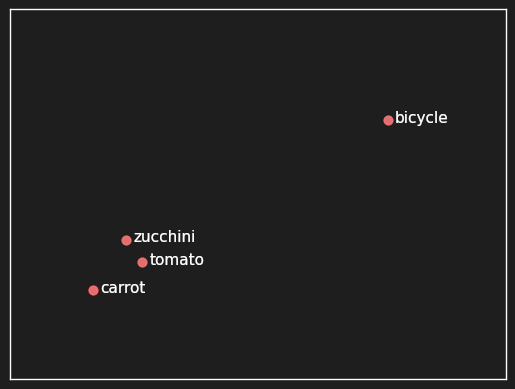
Similarly, we can often expect that words from the same semantic class, like tomato, carrot, and zucchini, appear in the same contexts:
- He grew tomatoes in his garden.
- He grew carrots in his garden.
- He grew zucchini in his garden.
But not:
- He grew bicycles in his garden.

Words that can fill the blank in “He grew _____ in his garden” share a property that they do not share with bicycles, and we can build an AI model that encompasses this information, along with thousands of other contexts where some words can go and others can’t.
Word embeddings are a way to encapsulate this information in a vector space.
tagImage Recognition
We can even construct embeddings where we don’t explicitly say what features are relevant.
For example, an embedding for a face recognition system translates pictures of people into embedding vectors distributed in a high-dimensional space.
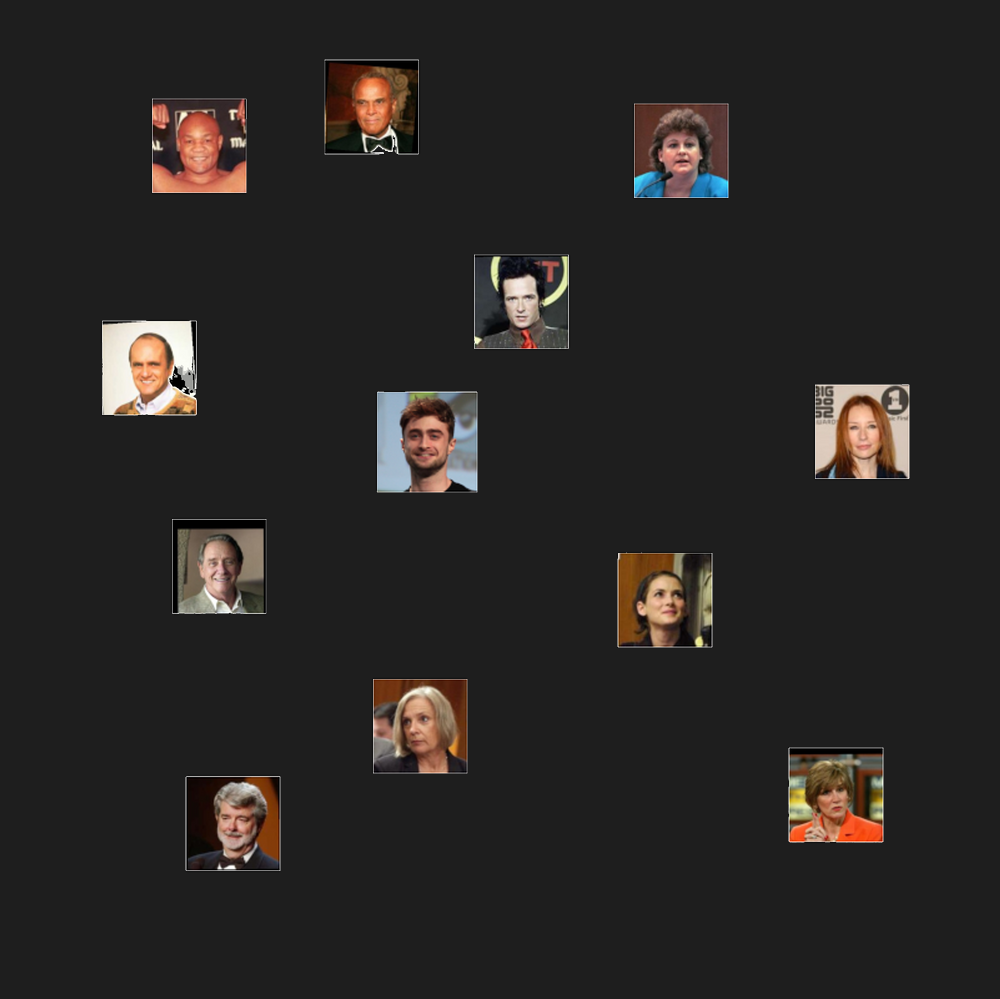
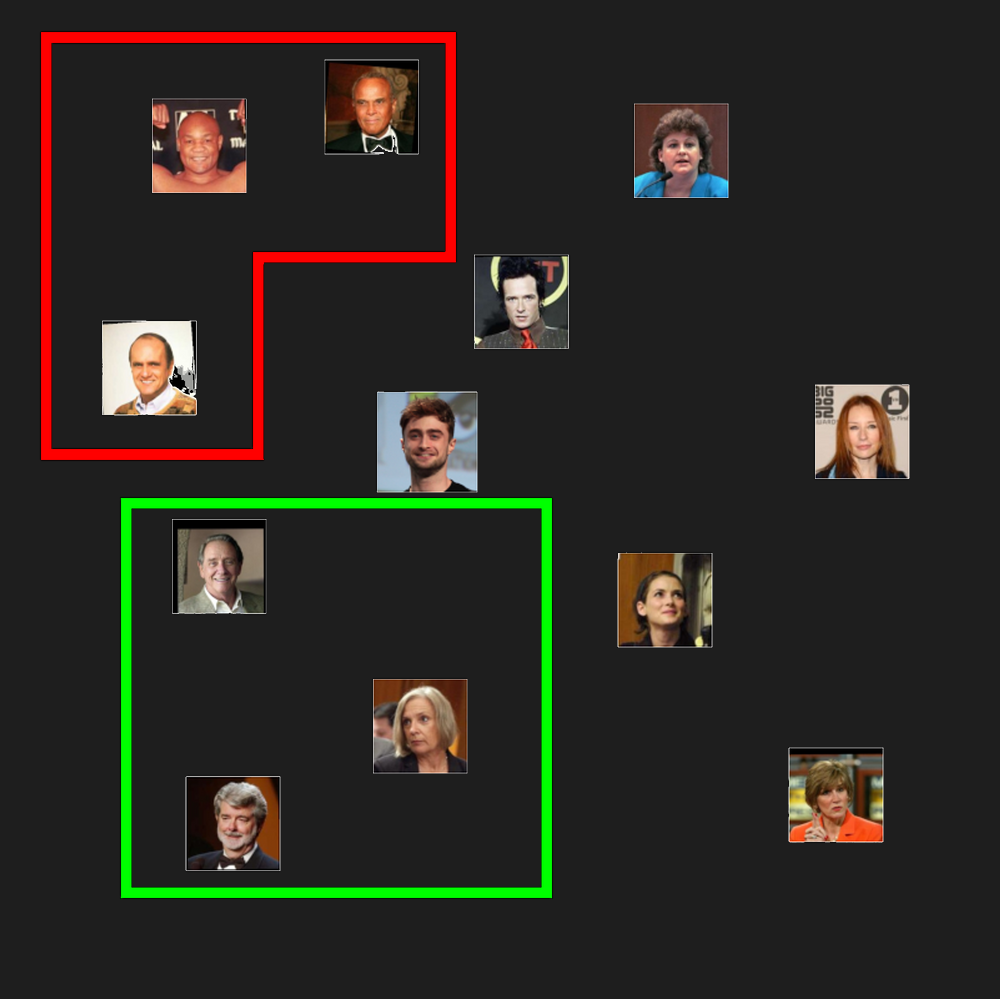
We might find that people whose faces have some common properties would be grouped together in some part of the embedding space. We might find, for example, that grey-haired people and bald people cluster together:
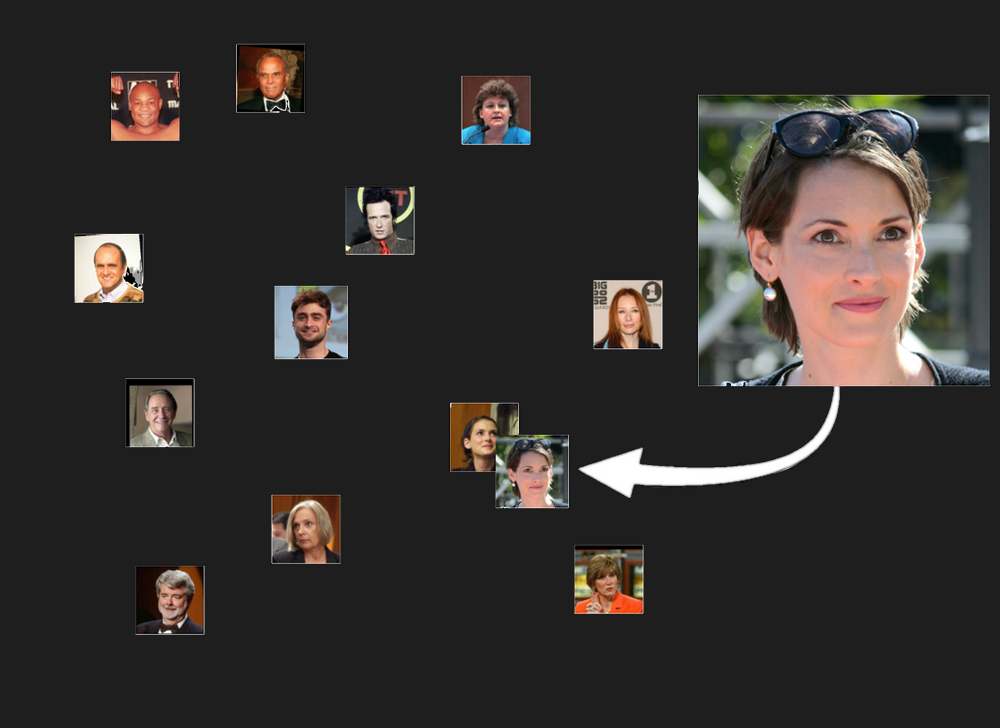
But more importantly and usefully, we would expect that if we gave it two pictures of the same person, those two embeddings would be closer to each other than to any other person’s picture:
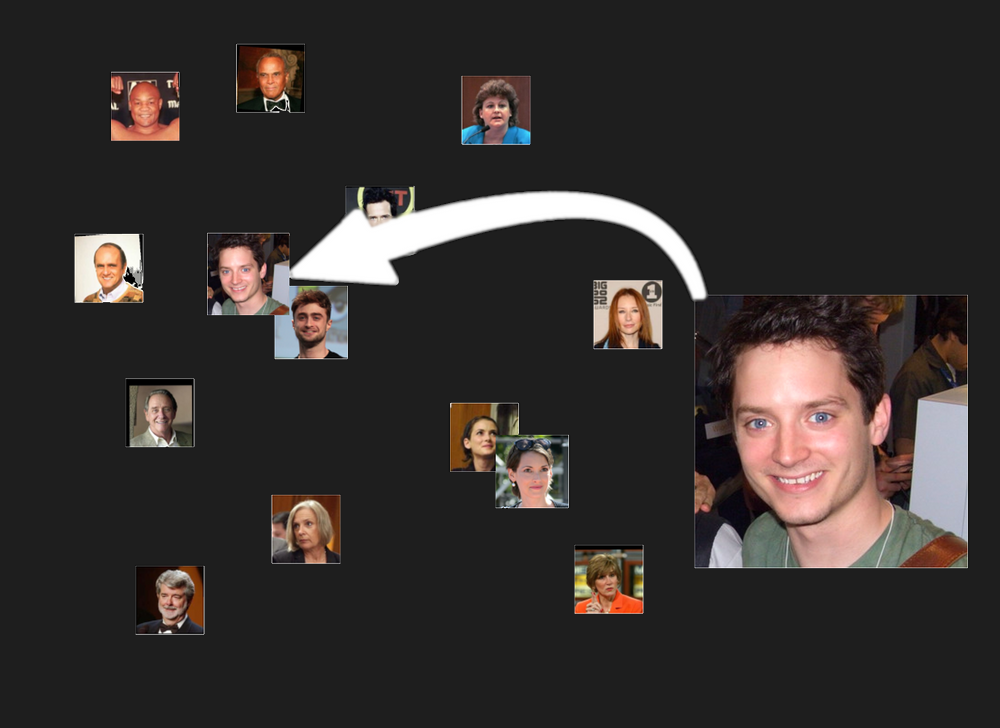
Of course, it would also find people who just look similar, although we hope that they wouldn’t be as close together as two people who are actually the same:
tagMultimodal Embeddings
Embedding spaces can also act as a bridge between different kinds of inputs.
For example, if we have a database of pictures with descriptive captions, we can co-train two embedding models — one for images and one for texts — to output vectors in the same embedding space. The result is that embeddings of descriptions of images and embeddings of the images themselves will be near each other.

tagEmbeddings Everywhere
Embeddings provide a very generalized framework for making useful comparisons between things. They are so useful that they see applications all over AI and machine learning. Any application that requires similarity/dissimilarity evaluation, relies on hidden or non-obvious features, or requires implicit context-sensitive mappings between different inputs and outputs, likely uses embeddings in some form.
They are actively in use for:
- Search and information retrieval for all media types
- Face and object recognition in machine vision
- Question-answering systems
- Recommender systems
- Outlier detection (often as part of fraud detection)
- Spellchecking and grammar correction
- Natural language understanding
- Machine translation
This is a far from exhaustive list because nearly every AI application uses embeddings. In some scenarios, embeddings are used internally and are invisible to users and developers, but many AI applications hinge on the ability to use embeddings to identify and compare things in useful, human-like ways.
Jina AI is developing a collection of high-performance specialized embedding models that you can download or use via our public API, without any of the complexities of AI development. We are also preparing a suite of open-source tools in Python to help you integrate embedding models into your tech stack.
Jina AI is committed to providing you with tools and help for creating, optimizing, evaluating, and implementing embedding models for your enterprise. We’re here to help you navigate the new world of business AI. Contact us via our website or join our community on Discord to get started.