We live in a “predictable” world of “logic”, where things go (more or less) as expected. Every day the sun rises, fish swim, birds fly, and people hurl abuse at each other on Twitter. Just another day on social media

If you drink more coffee, you get more hyper. If you browse more social media, you get more miserable. If you have a big problem and throw more CPUs at it, you get that problem solved more quickly.
One of these things is not like the others. Take a wild guess which.
Turns out that whole throwing CPUs at a problem thing? It doesn’t always work so well.
It should be straightforward. CPUs are just magical rocks full of lightning. More rocks should equal more speed. What the hell is happening here?
To start, let’s go back to the misty days of a few weeks ago, when our team was running some sharding experiments…
tagSharding
Katie is building a search engine for delicious cake recipes. There are a lot of cake recipes around the world, so she’ll soon have gazillions of recipes.

With Jina, that’s a piece of cake. The Jina framework supports sharding out of the box: when the data doesn't fit on one machine any more, Katie can split her data between multiple machines. She can do this split to speed up computation of a single request as well.

Let’s jump in and help Katie out. Maybe we’ll even get a guacamole donut for our troubles.
tagPreliminary testing
We wrote some benchmarking code that generates Documents with random embeddings and splits them between different shards of an indexer. We used that code to run a sharding experiment on an M2 mac.
import time
import numpy as np
from jina import Executor, requests, Flow, DocumentArray
top_k = 100
num_dim = 512
total_queries = 16
total_docs = 1_000_000
shards = 2
class MyExec1(Executor):
def __init__(self, **kwargs):
super().__init__(**kwargs)
num_docs = int(total_docs // shards)
self.da = DocumentArray.empty(num_docs)
self.da.embeddings = np.random.random((num_docs, num_dim)).astype(np.float32)
@requests
def foo(self, docs, **kwargs):
return self.da.find(docs, limit=int(top_k // shards), metric='cosine')[0]
f = Flow().add(uses=MyExec1, shards=shards, polling='all')
queries = DocumentArray.empty(total_queries)
queries.embeddings = np.random.random((total_queries, num_dim)).astype(np.float32)
with f:
st = time.perf_counter()
f.post('/', queries, request_size=1)
elapse = time.perf_counter() - st
qps = total_queries / elapseWe tested a variety of scenarios, with differing numbers of Documents and shards. For each scenario we:
- Created DocumentArrays with random 512-dimensional embeddings. The number of Documents varied between 10,000 and 1 million.
- Created a Flow with a single dummy indexer Executor. The shard count varied from 1 to 8.
- Ran several queries through the Flow and timed how long it took to get search results back.
Naturally, we assumed that more shards == better performance. Specifically, that querying Documents would be faster with more shards.
Well, you know what they say about “assume":

Needless to say, we didn’t get the results we expected:
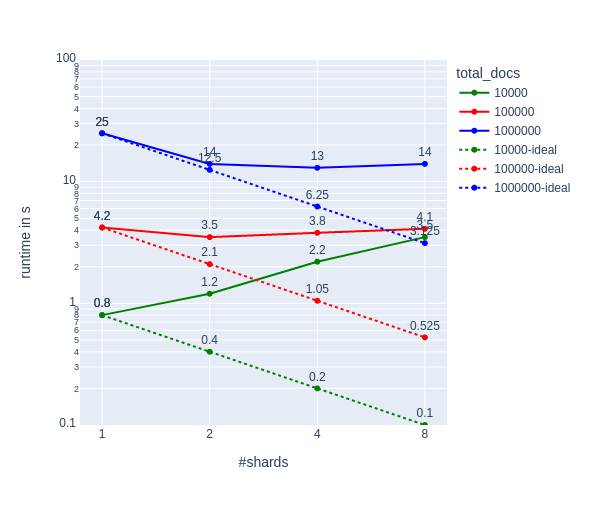
Not only did the shards not speed up the process as much as thought they should, but they actually slowed things down! C’mon shards, you had one job!
From the graph we can see:
- Sharding only makes sense when the overhead of sharding is smaller than the gain in multiprocessing. Sharding for 10,000 documents doesn’t make sense.
- Sharding beyond the number of cores in a machine brings no benefit. When CPU utilization hits 100% it’s pointless to split the task any further.
However, the line for 1 million Documents seems suspicious. Why don't we see any improvement when going from 2 to 4 shards?
tagJuicing up our testing
Let’s throw some serious compute at this baby and see what happens. I have an i9-12900KF with 16 cores and 24 threads under my desk. That amount of power should erase any bottlenecks for 4 shards, right?

In all experiments below, we did this:
- Create one DocumentArray consisting of 500,000 to 4 million Documents with random 512-dimension embeddings. Let’s call this the index.
- Create a Flow with a single dummy indexer Executor. The shard count varied from 1 to 8.
- Ran warm-up queries through the Flow. This ensures no initial hiccups in the benchmarking.
- Ran benchmark queries through the Flow. We used five queries, also with 512-dimension embeddings.
- Performed a
da.find()with both warm-up and benchmark queries. - Timed how long it took to run all five queries together.
Under the hood .find() calculates the cosine distance between the index embeddings and query embeddings. Be aware that .find() is designed for easy experimentation and not for big matrix multiplications in live systems. So don’t be shocked by the runtime below. Our target here is to analyze sharding and not to get the best performing vector search engine.
You can find all code in this repository:
tagExperiment 1: the basics
Let’s run two tests:
- 1A: 4 million docs in total with 1, 2, 4 or 8 shards. (total docs are constant, docs per shard varies)
- 1B: 500,000 docs per shard with 1, 2, 4 or 8 shards. (total docs vary, docs per shard is constant)
For each test, we run five queries. Our expectation would be to see the runtime halving for each step in 1A (blue) and a flat line for 1B (red).
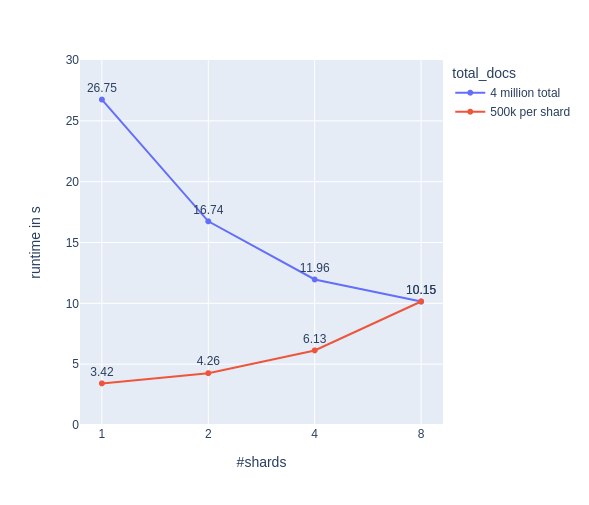
Hmmm…Not quite what we expected. Let’s have a quick look at htop for 1 and 4 shards in experiment 1B:
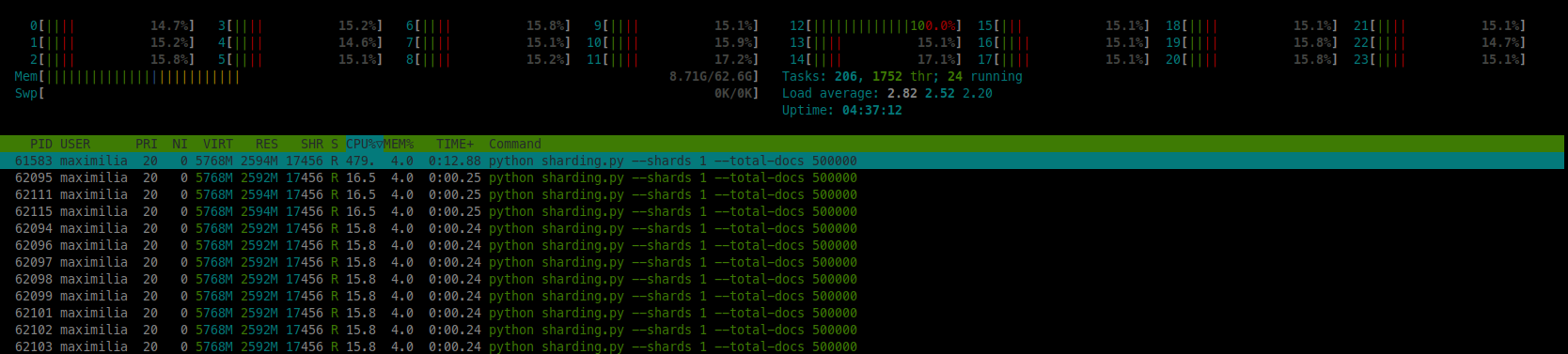
We see that NumPy does a pretty good job in multiprocessing itself. So when using 1 shard, we utilize ~4.5 CPUs and when using 4 shards we utilize ~8.75 CPUs. The total workload for 4 shards was 4 times as much as for 1 shard, and as such doubling the runtime seems to be legit.
tagExperiment 2: Disabling multiprocessing
Now let’s run the same experiment, with NumPy multiprocessing turned off:
os.environ['OPENBLAS_NUM_THREADS'] = '1'
os.environ['MKL_NUM_THREADS'] = '1'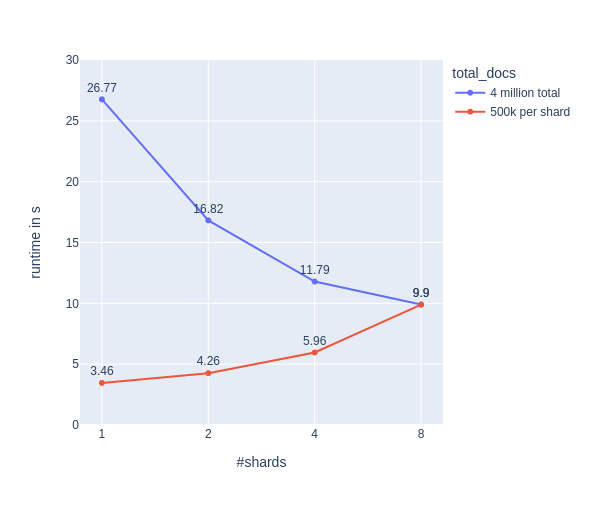
Whoopsie! Yes, this is almost the very same result as above. Did we really disable multiprocessing? Let’s have a look at htop again for one shard:

Yes, there really is only one core utilized. So NumPy performs the computation at the same speed regardless of whether it’s fully using 4.5 cores or just one.
Perhaps the main computation isn’t even the cosine distance computation. Luckily, our core team just implemented tracing for Jina. Let’s take a look at the “search” span:
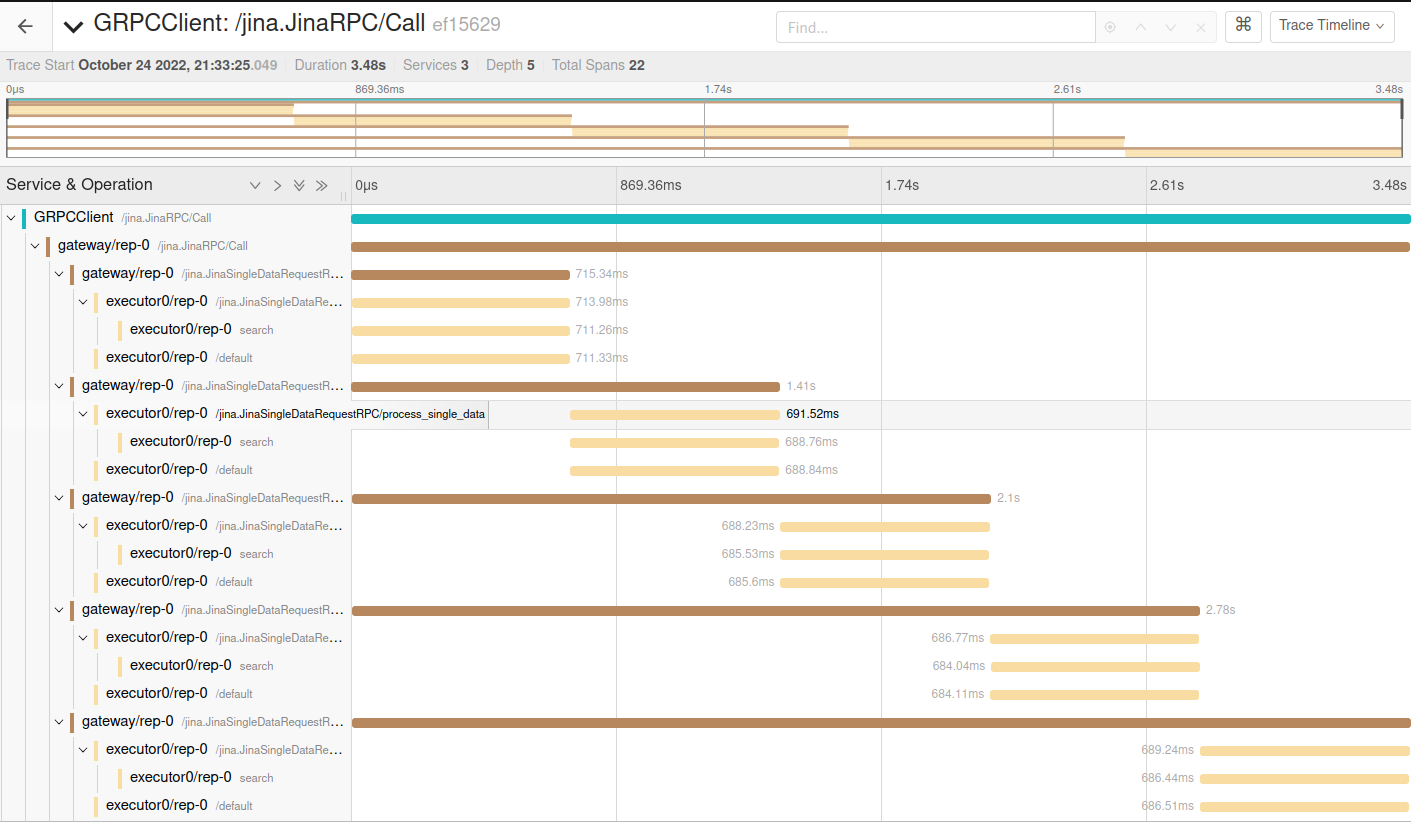
We can see my five requests and how they’re sequentially processed. The “search” span is where all the computation happens and takes almost all the time. So we have certainty that the main computation is the cosine distance. Our sharding seems to work just fine.
tagMy theory
I’m very grateful that I saw similar behavior some years ago. At that time, Bill de hÓra (as a senior architect) took time to give me a hint to the solution. I’m no expert in low-level processor architecture, but let me give you my understanding of what just happened:
When you parallelize memory- and CPU-intensive workloads on a single physical chip, each processor needs to load the to-be-processed data into the lowest level cache (L1 cache). When a single core needs more than 1/(utilized cores) of the L1 cache, the processors do their computations in a kind of round-robin fashion, constantly interrupting each other. By doing that, they are busier reloading data into the cache than performing actual computation. My processor’s specs say “Max Memory Bandwidth: 76.8 GB/s”, which should ensure I can load all the needed data into the cache in a fraction of a second.
My guess: the individual cores interrupt each other so often that they are busier loading from memory than doing the actual computation.
tagVerifying my theory: Different plain matrix multiplications
Let's try different matrix multiplications.
- A: (2,000,000, 100) * (100, 100) ⇒ 2,000,000*100*100 = 2*10^10 operations
- B: (3,000, 3,000) * (3,000, 3,000) ⇒ 3,000*3,000*3,000 = 2.7*10^10 operations
The data loading for the same amount of basic multiplications in both cases roughly looks like this:
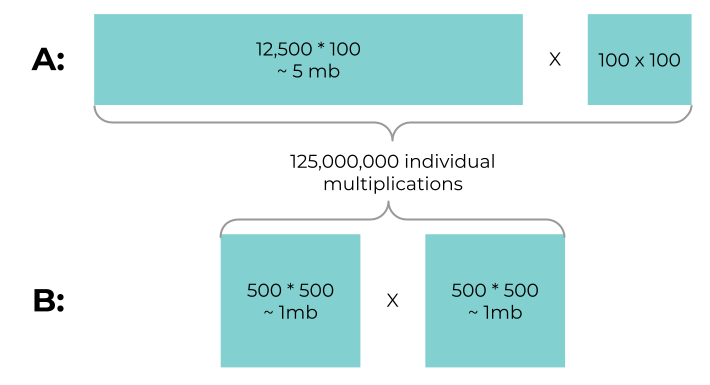
We need to load 2.5 times more data into the cache for the same amount of operations. Therefore the individual cores are more likely to need to do memory swapping.
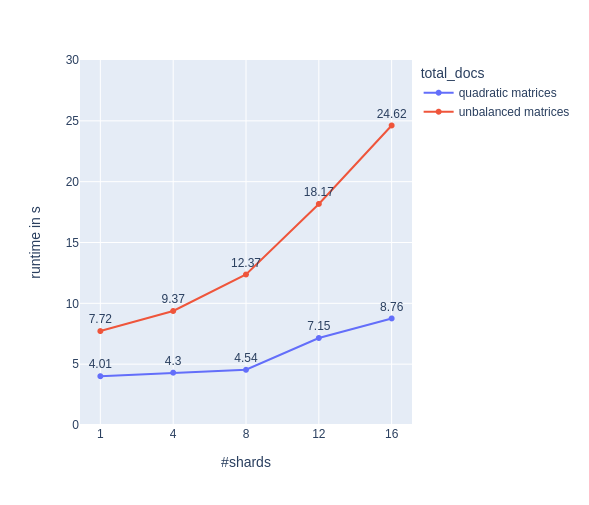
For unbalanced matrices we see the same behavior as in our da.find() experiment above. For quadratic matrices we see, that up to 8 shards there’s only a small increase in runtime and the shards behave well. I can’t judge if the runtime increases beyond 8 shards for quadratic matrices due to having only 8 high-performance CPUs and 8 low-performance CPUs, or in having the decreased part of the cache that every shard gets.
Oh, I almost forgot to mention: This experiment also shows us the bad behavior doesn’t come from the small overhead that our DocumentArray produces. Lucky us!
I also ran experiment 1B with AnnLite to see how sharding behaves with a proper implementation of HNSW (a very common vector search algorithm).
The outcome: sharding had no impact on the runtime. Tracing showed that the actual computation was blazingly fast (under 3ms). Furthermore, tracing showed that the actual computations really ran in parallel and didn’t affect each other’s runtimes.
tagConclusion
Luckily for us, sharding works just fine in a real world scenario. In a future post we’ll look at sharding across different machines. Given the traces above (and a lot of other traces I looked upon during the process) it should work just fine.
But multiprocessing memory- and CPU-intensive work on one machine is tricky. What I find really concerning: A lot of computations are run on the cloud, where we have no control over the hardware.
Coming back to our cake search engine: Let’s say Katie’s company is starting to grow and wants to run the service on the cloud, via multiple virtual machines. There’s no guarantee that these are independent physical machines - they could all be running on the same box with the same L1 cache, and thus ruin Katie’s performance. That would really leave a bad taste in her mouth.

Perhaps worse: When using Kubernetes we often explicitly have multiple Pods on the same machine. Even when the neighbors are not noisy in the sense of over-utilizing CPU/memory resources, they can have a workload that does bad things to low-level cache or another non-obvious resource and slow neighbors down.
Do you like the post, or think my low-level cache analysis or conclusion is wrong? Talk to me in the comments or on Twitter.





