Embeddings стали краеугольным камнем множества приложений искусственного интеллекта и обработки естественного языка, предоставляя способ представления значений текстов в виде многомерных векторов. Однако с увеличением размера моделей и растущим объемом данных, обрабатываемых моделями ИИ, вычислительные требования и требования к хранению для традиционных embeddings возросли. Binary embeddings были представлены как компактная, эффективная альтернатива, которая сохраняет высокую производительность при значительном снижении требований к ресурсам.
Binary embeddings — это один из способов смягчить эти требования к ресурсам, уменьшая размер векторов embeddings до 96% (96.875% в случае Jina Embeddings). Пользователи могут использовать мощь компактных binary embeddings в своих ИИ-приложениях с минимальной потерей точности.
tagЧто такое Binary Embeddings?
Binary embeddings — это специализированная форма представления данных, где традиционные многомерные векторы с плавающей точкой преобразуются в бинарные векторы. Это не только сжимает embeddings, но и сохраняет практически всю целостность и полезность векторов. Суть этой техники заключается в её способности сохранять семантику и относительные расстояния между точками данных даже после преобразования.
Магия binary embeddings заключается в квантизации — методе, который превращает числа высокой точности в числа с меньшей точностью. В моделировании ИИ это часто означает преобразование 32-битных чисел с плавающей точкой в embeddings в представления с меньшим количеством битов, например, 8-битные целые числа.

Binary embeddings доводят это до крайности, сводя каждое значение к 0 или 1. Преобразование 32-битных чисел с плавающей точкой в бинарные цифры уменьшает размер векторов embeddings в 32 раза, сокращение на 96.875%. В результате векторные операции с полученными embeddings происходят намного быстрее. Использование аппаратных ускорений, доступных на некоторых микрочипах, может увеличить скорость сравнения векторов гораздо больше чем в 32 раза, когда векторы бинаризованы.
Некоторая информация неизбежно теряется в этом процессе, но эта потеря минимизируется, когда модель очень эффективна. Если non-quantized embeddings разных вещей максимально различны, то бинаризация с большей вероятностью хорошо сохранит эту разницу. В противном случае может быть сложно правильно интерпретировать embeddings.
Модели Jina Embeddings обучены быть очень устойчивыми именно таким образом, что делает их хорошо подходящими для бинаризации.
Такие компактные embeddings делают возможными новые приложения ИИ, особенно в контекстах с ограниченными ресурсами, таких как мобильные и чувствительные ко времени приложения.
Эти преимущества в стоимости и времени вычислений достигаются при относительно небольших потерях в производительности, как показано на графике ниже.

Для jina-embeddings-v2-base-en бинарная квантизация снижает точность поиска с 47.13% до 42.05%, потеря примерно 10%. Для jina-embeddings-v2-base-de эта потеря составляет всего 4%, с 44.39% до 42.65%.
Модели Jina Embeddings так хорошо работают при создании бинарных векторов, потому что они обучены создавать более равномерное распределение embeddings. Это означает, что два разных embeddings будут вероятнее всего дальше друг от друга в большем количестве измерений, чем embeddings из других моделей. Это свойство обеспечивает лучшее представление этих расстояний в их бинарной форме.
tagКак работают Binary Embeddings?
Чтобы понять, как это работает, рассмотрим три embedding: A, B и C. Все три являются полными векторами с плавающей точкой, не бинаризованными. Допустим, расстояние от A до B больше, чем расстояние от B до C. С embeddings мы обычно используем косинусное расстояние, поэтому:
Если мы бинаризуем A, B и C, мы можем измерить расстояние более эффективно с помощью расстояния Хэмминга.
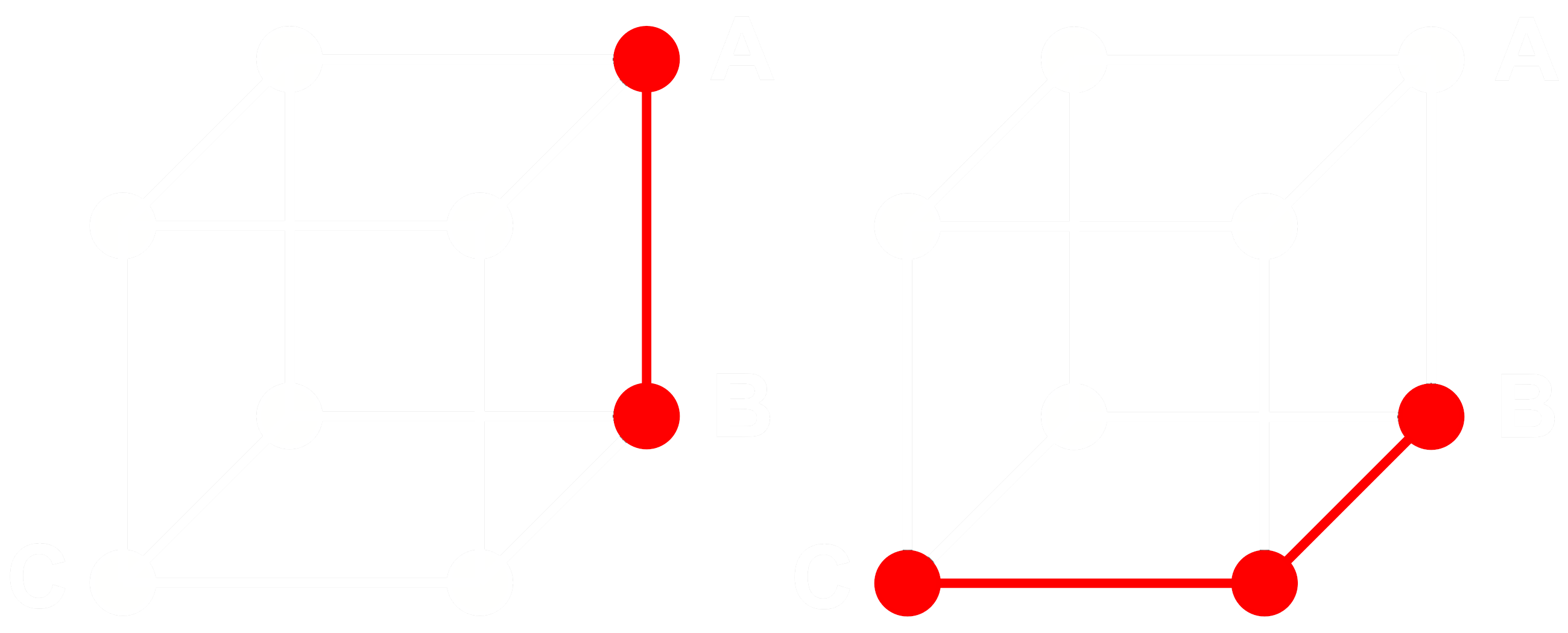
Назовем Abin, Bbin и Cbin бинаризованными версиями A, B и C.
Для бинарных векторов, если косинусное расстояние между Abin и Bbin больше, чем между Bbin и Cbin, тогда расстояние Хэмминга между Abin и Bbin больше или равно расстоянию Хэмминга между Bbin и Cbin.
Таким образом, если:
тогда для расстояний Хэмминга:
В идеале, когда мы бинаризуем embeddings, мы хотим, чтобы те же отношения с полными embeddings сохранялись для бинарных embeddings, как и для полных. Это означает, что если одно расстояние больше другого для косинуса с плавающей точкой, оно должно быть больше для расстояния Хэмминга между их бинаризованными эквивалентами:
Мы не можем сделать это верным для всех троек embeddings, но можем сделать это верным почти для всех из них.
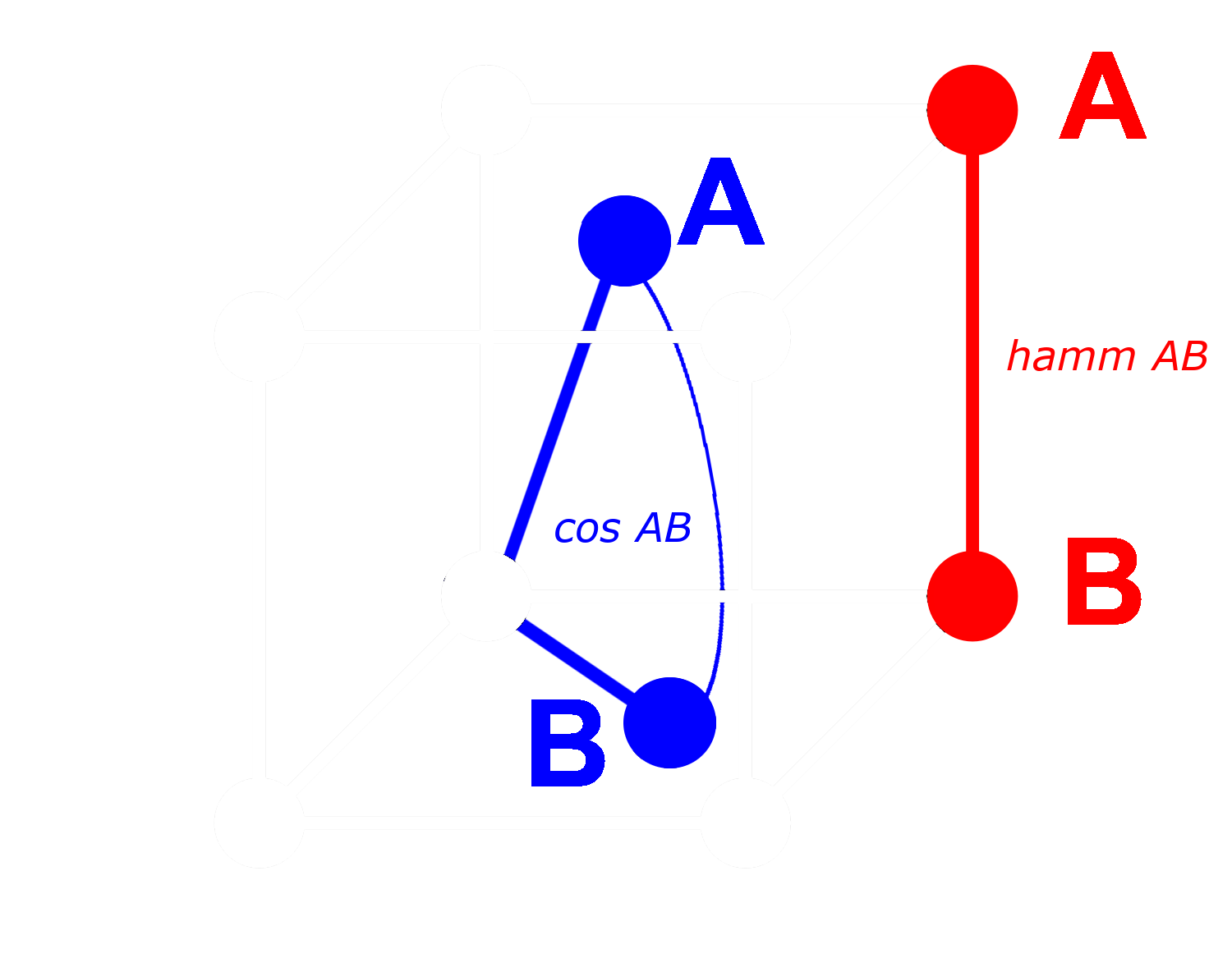
С бинарным вектором мы можем рассматривать каждое измерение как присутствующее (единица) или отсутствующее (ноль). Чем дальше два вектора друг от друга в небинарной форме, тем выше вероятность того, что в любом одном измерении у одного будет положительное значение, а у другого — отрицательное. Это означает, что в бинарной форме, скорее всего, будет больше измерений, где у одного будет ноль, а у другого — единица. Это делает их дальше друг от друга по расстоянию Хэмминга.
Противоположное применимо к векторам, которые ближе друг к другу: Чем ближе небинарные векторы, тем выше вероятность того, что в любом измерении у обоих будут нули или у обоих будут единицы. Это делает их ближе по расстоянию Хэмминга.
Модели Jina Embeddings так хорошо подходят для бинаризации, потому что мы обучаем их с использованием negative mining и других практик тонкой настройки, чтобы особенно увеличить расстояние между непохожими вещами и уменьшить расстояние между похожими. Это делает embeddings более устойчивыми, более чувствительными к сходствам и различиям, и делает расстояние Хэмминга между бинарными embeddings более пропорциональным косинусному расстоянию между небинарными.
tagСколько можно сэкономить с Binary Embeddings от Jina AI?
Использование моделей binary embedding от Jina AI не только снижает задержку в чувствительных ко времени приложениях, но также дает значительные преимущества в стоимости, как показано в таблице ниже:
| Model | Memory per 250 million embeddings |
Retrieval benchmark average |
Estimated price on AWS ($3.8 per GB/month with x2gb instances) |
|---|---|---|---|
| 32-bit floating point embeddings | 715 GB | 47.13 | $35,021 |
| Binary embeddings | 22.3 GB | 42.05 | $1,095 |
Это сокращение более чем на 95% сопровождается лишь ~10% снижением точности поиска.
Эта экономия даже больше, чем при использовании бинаризованных векторов из модели OpenAI Ada 2 или Cohere Embed v3, которые производят эмбеддинги размерностью 1024 или более. Эмбеддинги Jina AI имеют только 768 измерений и при этом работают сопоставимо с другими моделями, делая их меньше даже до квантования при той же точности.
Эта экономия также экологична, используя меньше редких материалов и энергии.
tagНачало работы
Чтобы получить бинарные эмбеддинги с помощью Jina Embeddings API, просто добавьте параметр encoding_type в ваш API-запрос, со значением binary для получения бинаризованного эмбеддинга, закодированного как знаковые целые числа, или ubinary для беззнаковых целых чисел.
tagПрямой доступ к Jina Embedding API
Использование curl:
curl https://api.jina.ai/v1/embeddings \
-H "Content-Type: application/json" \
-H "Authorization: Bearer <YOUR API KEY>" \
-d '{
"input": ["Your text string goes here", "You can send multiple texts"],
"model": "jina-embeddings-v2-base-en",
"encoding_type": "binary"
}'
Или через Python API requests:
import requests
headers = {
"Content-Type": "application/json",
"Authorization": "Bearer <YOUR API KEY>"
}
data = {
"input": ["Your text string goes here", "You can send multiple texts"],
"model": "jina-embeddings-v2-base-en",
"encoding_type": "binary",
}
response = requests.post(
"https://api.jina.ai/v1/embeddings",
headers=headers,
json=data,
)
С помощью вышеприведенного Python request вы получите следующий ответ при проверке response.json():
{
"model": "jina-embeddings-v2-base-en",
"object": "list",
"usage": {
"total_tokens": 14,
"prompt_tokens": 14
},
"data": [
{
"object": "embedding",
"index": 0,
"embedding": [
-0.14528547,
-1.0152762,
...
]
},
{
"object": "embedding",
"index": 1,
"embedding": [
-0.109809875,
-0.76077706,
...
]
}
]
}
Это два бинарных вектора эмбеддинга, хранящиеся как 96 8-битных знаковых целых чисел. Чтобы распаковать их в 768 нулей и единиц, вам нужно использовать библиотеку numpy:
import numpy as np
# assign the first vector to embedding0
embedding0 = response.json()['data'][0]['embedding']
# convert embedding0 to a numpy array of unsigned 8-bit ints
uint8_embedding = np.array(embedding0).astype(numpy.uint8)
# unpack to binary
np.unpackbits(uint8_embedding)
Результат - это 768-мерный вектор, содержащий только 0 и 1:
array([0, 0, 1, 1, 0, 1, 1, 0, 1, 1, 0, 0, 0, 1, 0, 1, 1, 1, 1, 1, 0, 0,
0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 1, 1, 0, 0, 0, 1, 1, 1, 0, 1, 0, 1,
0, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 1, 1, 0, 0, 0, 0, 1, 0, 1, 1, 1,
0, 0, 0, 0, 1, 1, 1, 0, 0, 1, 0, 0, 0, 0, 1, 1, 1, 1, 0, 1, 0, 1,
1, 1, 0, 1, 1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 0, 0, 0,
0, 0, 1, 0, 0, 0, 1, 0, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1, 0, 0, 1, 0,
1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 1,
1, 0, 1, 0, 1, 1, 0, 0, 0, 1, 0, 1, 1, 1, 0, 0, 1, 1, 0, 0, 0, 1,
1, 1, 0, 1, 0, 1, 1, 1, 1, 0, 1, 0, 0, 1, 0, 0, 1, 0, 1, 0, 1, 1,
0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 1, 1, 0, 1, 0, 0, 0, 1, 1, 1,
1, 0, 0, 1, 0, 0, 0, 1, 0, 1, 0, 0, 1, 0, 1, 0, 1, 0, 0, 1, 0, 0,
0, 0, 0, 0, 1, 0, 0, 0, 1, 1, 1, 0, 1, 1, 0, 1, 1, 0, 1, 0, 0, 0,
1, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1, 1, 0, 1, 1, 0, 0, 0, 1, 0, 0, 1,
0, 0, 0, 0, 0, 1, 1, 0, 0, 1, 1, 1, 1, 0, 1, 0, 1, 0, 1, 1, 1, 1,
1, 0, 1, 0, 0, 0, 1, 0, 0, 1, 0, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 0,
0, 0, 0, 0, 1, 0, 1, 1, 1, 0, 1, 1, 1, 1, 0, 0, 0, 0, 0, 1, 1, 1,
1, 1, 1, 1, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 1, 0, 1, 0, 1,
1, 0, 1, 1, 1, 0, 0, 1, 0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 0, 0, 1, 1,
0, 0, 0, 1, 1, 1, 1, 1, 0, 1, 1, 0, 1, 0, 0, 0, 1, 1, 0, 1, 1, 0,
1, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 1, 1, 1, 0, 1, 1, 1, 0,
0, 0, 0, 0, 0, 1, 1, 1, 1, 0, 1, 0, 1, 1, 0, 1, 0, 1, 1, 1, 0, 0,
0, 0, 1, 1, 1, 0, 1, 0, 1, 0, 0, 1, 0, 1, 0, 0, 0, 1, 1, 1, 0, 1,
0, 1, 1, 1, 0, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 0, 0, 1, 0,
0, 1, 1, 1, 0, 1, 1, 0, 0, 1, 1, 0, 1, 1, 0, 1, 1, 1, 0, 1, 1, 0,
1, 1, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 1, 1, 1, 0, 1, 1, 0,
0, 1, 0, 0, 1, 1, 0, 1, 0, 0, 1, 0, 0, 1, 0, 1, 0, 1, 1, 1, 0, 0,
0, 0, 1, 1, 0, 1, 0, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 0, 1,
1, 0, 1, 1, 0, 1, 1, 0, 1, 0, 0, 1, 0, 0, 0, 1, 0, 1, 0, 1, 1, 0,
1, 1, 1, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1, 0, 0, 1, 0, 1, 1, 0, 0,
1, 0, 1, 1, 1, 1, 1, 1, 1, 0, 1, 0, 0, 0, 1, 0, 0, 1, 1, 1, 0, 1,
1, 1, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 1, 1, 0, 1, 1, 0, 0, 1, 1, 0,
1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 1, 0, 0, 1, 1, 0, 1,
1, 1, 1, 0, 0, 1, 1, 1, 0, 1, 0, 0, 1, 1, 0, 1, 1, 1, 1, 1, 1, 0,
1, 1, 1, 0, 0, 1, 1, 0, 0, 1, 0, 0, 1, 1, 0, 0, 0, 1, 0, 1, 1, 1,
0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 0, 1, 0, 0],
dtype=uint8)
tagИспользование бинарного квантования в Qdrant
Вы также можете использовать интеграционную библиотеку Qdrant для прямого размещения бинарных эмбеддингов в вашем векторном хранилище Qdrant. Поскольку Qdrant внутренне реализовал BinaryQuantization, вы можете использовать его как предустановленную конфигурацию для всей векторной коллекции, что позволяет извлекать и хранить бинарные векторы без каких-либо других изменений в вашем коде.
Смотрите пример кода ниже, как это сделать:
import qdrant_client
import requests
from qdrant_client.models import Distance, VectorParams, Batch, BinaryQuantization, BinaryQuantizationConfig
# Укажите API-ключ Jina и выберите одну из доступных моделей.
# Вы можете получить пробный ключ здесь: https://jina.ai/embeddings/
JINA_API_KEY = "jina_xxx"
MODEL = "jina-embeddings-v2-base-en" # или "jina-embeddings-v2-base-en"
EMBEDDING_SIZE = 768 # 512 для малого варианта
# Получаем эмбеддинги через API
url = "https://api.jina.ai/v1/embeddings"
headers = {
"Content-Type": "application/json",
"Authorization": f"Bearer {JINA_API_KEY}",
}
text_to_encode = ["Your text string goes here", "You can send multiple texts"]
data = {
"input": text_to_encode,
"model": MODEL,
}
response = requests.post(url, headers=headers, json=data)
embeddings = [d["embedding"] for d in response.json()["data"]]
# Индексируем эмбеддинги в Qdrant
client = qdrant_client.QdrantClient(":memory:")
client.create_collection(
collection_name="MyCollection",
vectors_config=VectorParams(size=EMBEDDING_SIZE, distance=Distance.DOT, on_disk=True),
quantization_config=BinaryQuantization(binary=BinaryQuantizationConfig(always_ram=True)),
)
client.upload_collection(
collection_name="MyCollection",
ids=list(range(len(embeddings))),
vectors=embeddings,
payload=[
{"text": x} for x in text_to_encode
],
)Для настройки поиска следует использовать параметры oversampling и rescore:
from qdrant_client.models import SearchParams, QuantizationSearchParams
results = client.search(
collection_name="MyCollection",
query_vector=embeddings[0],
search_params=SearchParams(
quantization=QuantizationSearchParams(
ignore=False,
rescore=True,
oversampling=2.0,
)
)
)tagИспользование LlamaIndex
Чтобы использовать бинарные эмбеддинги Jina с LlamaIndex, установите параметр encoding_queries в значение binary при создании объекта JinaEmbedding:
from llama_index.embeddings.jinaai import JinaEmbedding
# Вы можете получить пробный ключ на https://jina.ai/embeddings/
JINA_API_KEY = "<YOUR API KEY>"
jina_embedding_model = JinaEmbedding(
api_key=jina_ai_api_key,
model="jina-embeddings-v2-base-en",
encoding_queries='binary',
encoding_documents='float'
)
jina_embedding_model.get_query_embedding('Query text here')
jina_embedding_model.get_text_embedding_batch(['X', 'Y', 'Z'])
tagДругие векторные базы данных с поддержкой бинарных эмбеддингов
Следующие векторные базы данных обеспечивают нативную поддержку бинарных векторов:
tagПример
Чтобы продемонстрировать бинарные эмбеддинги в действии, мы взяли подборку аннотаций с arXiv.org и получили для них как 32-битные векторы с плавающей точкой, так и бинарные векторы, используя jina-embeddings-v2-base-en. Затем мы сравнили их с эмбеддингами для примера запроса: "3D segmentation".
Как видно из таблицы ниже, первые три ответа совпадают, и четыре из пяти лучших совпадений одинаковы. Использование бинарных векторов дает практически идентичные топовые совпадения.
| Binary | 32-bit Float | |||
|---|---|---|---|---|
| Rank | Hamming dist. |
Matching Text | Cosine | Matching text |
| 1 | 0.1862 | SEGMENT3D: A Web-based Application for Collaboration... |
0.2340 | SEGMENT3D: A Web-based Application for Collaboration... |
| 2 | 0.2148 | Segmentation-by-Detection: A Cascade Network for... |
0.2857 | Segmentation-by-Detection: A Cascade Network for... |
| 3 | 0.2174 | Vox2Vox: 3D-GAN for Brain Tumour Segmentation... |
0.2973 | Vox2Vox: 3D-GAN for Brain Tumour Segmentation... |
| 4 | 0.2318 | DiNTS: Differentiable Neural Network Topology Search... |
0.2983 | Anisotropic Mesh Adaptation for Image Segmentation... |
| 5 | 0.2331 | Data-Driven Segmentation of Post-mortem Iris Image... |
0.3019 | DiNTS: Differentiable Neural Network Topology... |