Embeddings 已成為多種人工智慧和自然語言處理應用的基石,提供了一種將文本含義表示為高維向量的方法。然而,隨著模型規模的增長和人工智慧模型處理的數據量增加,傳統 embeddings 的計算和儲存需求也隨之攀升。Binary embeddings 作為一種緊湊高效的替代方案被引入,在大幅降低資源需求的同時仍能保持高性能。
Binary embeddings 是一種降低資源需求的方法,可以將 embedding 向量的大小減少高達 96%(在 Jina Embeddings 的情況下可達 96.875%)。用戶可以在其人工智慧應用中利用緊湊的 binary embeddings 的優勢,同時將精確度損失降到最低。
tag什麼是 Binary Embeddings?
Binary embeddings 是一種特殊的數據表示形式,將傳統的高維浮點向量轉換為二進制向量。這不僅壓縮了 embeddings,還保留了幾乎所有向量的完整性和實用性。這種技術的精髓在於即使在轉換後仍能保持數據點之間的語義和關係距離。
Binary embeddings 背後的魔力在於量化,這是一種將高精度數字轉換為低精度數字的方法。在人工智慧建模中,這通常意味著將 embeddings 中的 32 位浮點數轉換為較少位元的表示形式,如 8 位整數。

Binary embeddings 將這一過程推向極致,將每個值簡化為 0 或 1。將 32 位浮點數轉換為二進制位元可以將 embedding 向量的大小減少 32 倍,減少幅度達 96.875%。因此,在轉換後的 embeddings 上進行向量運算會快得多。在某些微晶片上使用硬體加速可以使二值化向量的比較速度提升超過 32 倍。
在這個過程中難免會損失一些資訊,但當模型性能很好時,這種損失可以降到最低。如果不同事物的非量化 embeddings 有最大的差異,那麼二值化更有可能很好地保留這種差異。否則,就很難正確解釋這些 embeddings。
Jina Embeddings 模型在這方面訓練得非常穩健,使其特別適合二值化。
這種緊湊的 embeddings 使得新的人工智慧應用成為可能,特別是在資源受限的環境中,如移動設備和時間敏感的應用場景。
如下圖所示,這些成本和運算時間的優勢僅帶來相對較小的性能損失。

對於 jina-embeddings-v2-base-en,二值量化將檢索準確率從 47.13% 降低到 42.05%,損失約 10%。對於 jina-embeddings-v2-base-de,這種損失僅為 4%,從 44.39% 降至 42.65%。
Jina Embeddings 模型在生成二進制向量時表現如此出色,是因為它們經過訓練可以創建更均勻分布的 embeddings。這意味著與其他模型的 embeddings 相比,兩個不同的 embeddings 在更多維度上可能會相距更遠。這種特性確保了這些距離能更好地通過二進制形式來表示。
tagBinary Embeddings 如何運作?
為了理解其工作原理,考慮三個 embeddings:A、B 和 C。這三個都是完整的浮點向量,而不是二值化的向量。現在,假設 A 到 B 的距離大於 B 到 C 的距離。對於 embeddings,我們通常使用餘弦距離,所以:
如果我們將 A、B 和 C 二值化,我們可以使用漢明距離更有效地測量距離。
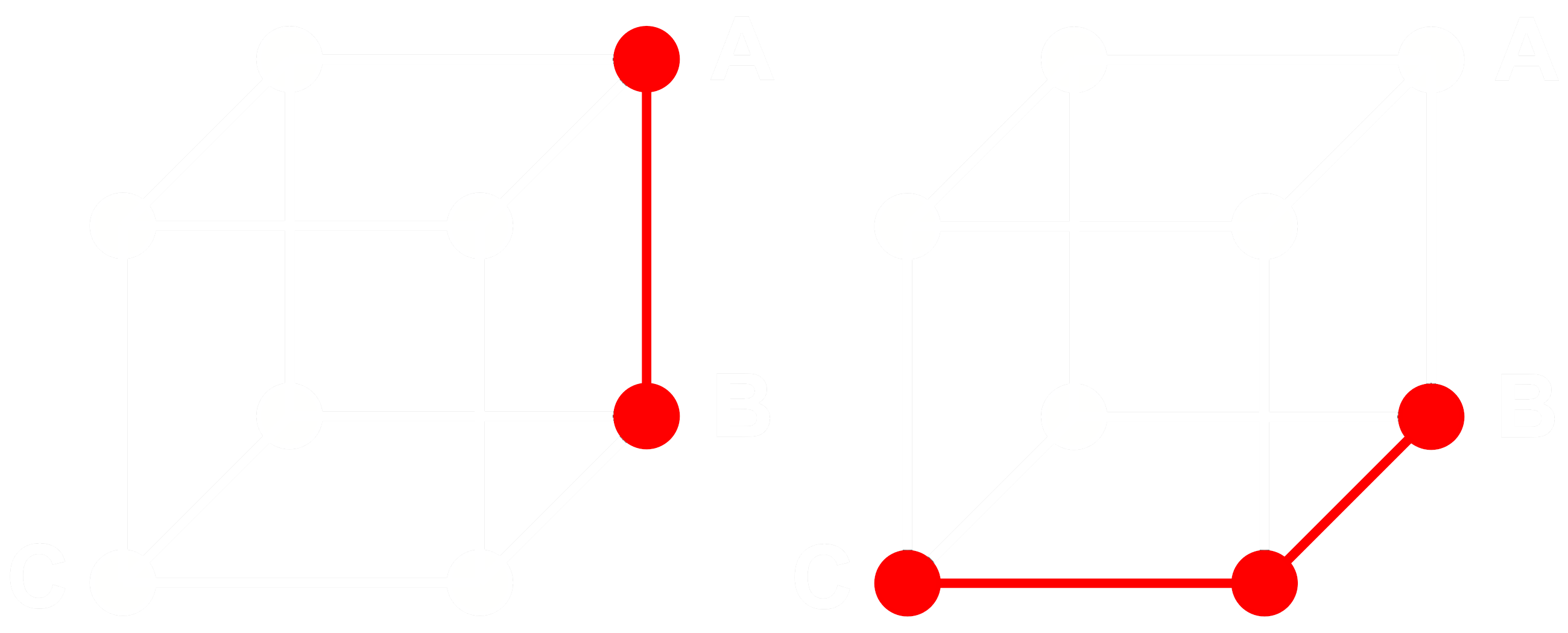
讓我們把 A、B 和 C 的二值化版本稱為 Abin、Bbin 和 Cbin。
對於二進制向量,如果 Abin 和 Bbin 之間的餘弦距離大於 Bbin 和 Cbin 之間的距離,那麼 Abin 和 Bbin 之間的漢明距離大於或等於 Bbin 和 Cbin 之間的漢明距離。
所以如果:
那麼對於漢明距離:
理想情況下,當我們對 embeddings 進行二值化時,我們希望完整 embeddings 之間的相同關係在二進制 embeddings 中也成立。這意味著如果一個浮點餘弦距離大於另一個,那麼它們二值化版本之間的漢明距離也應該更大:
我們無法對所有 embeddings 三元組都實現這一點,但我們可以使其對幾乎所有三元組都成立。
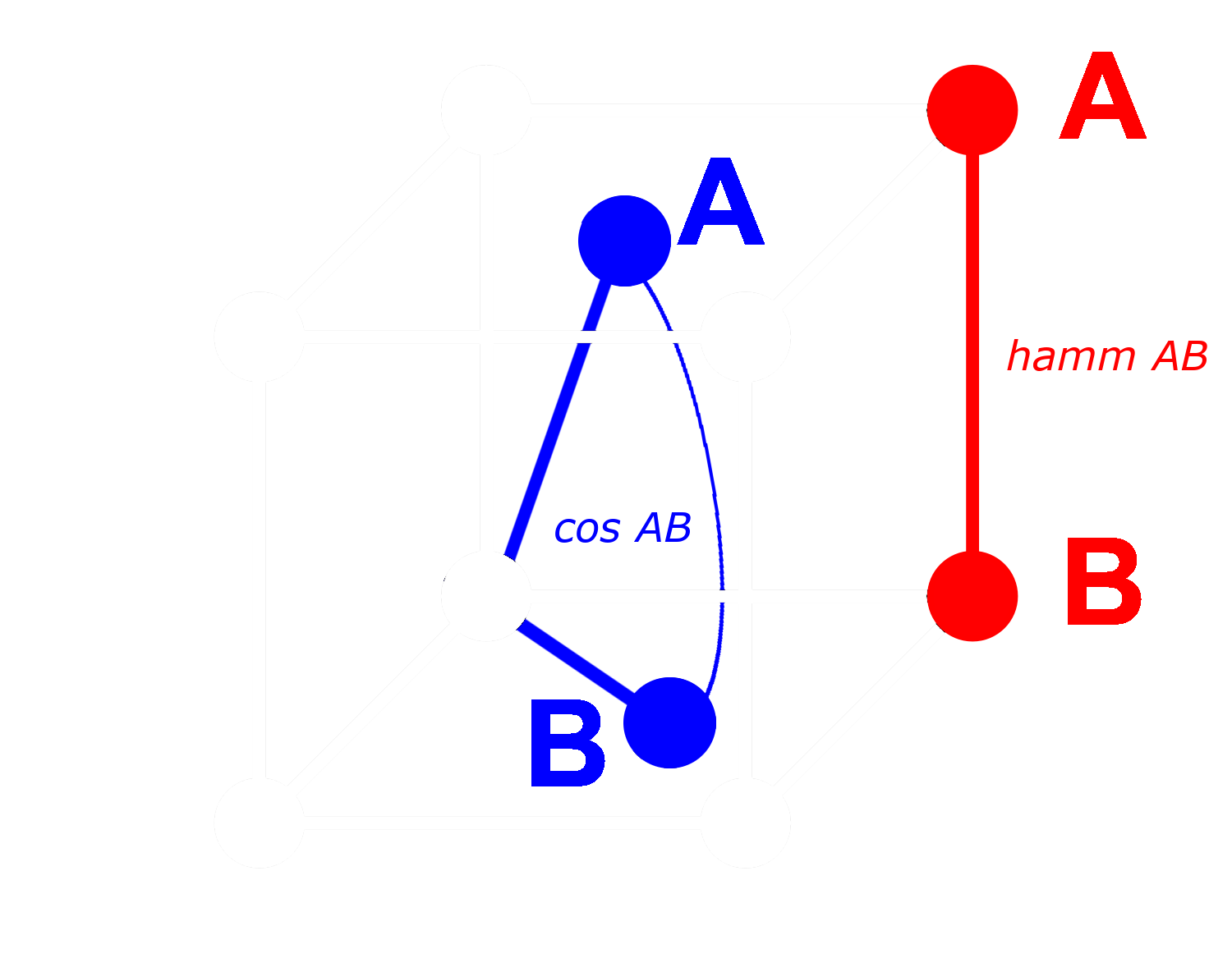
對於二進制向量,我們可以將每個維度視為存在(1)或不存在(0)。兩個向量在非二進制形式中的距離越遠,在任一維度上一個有正值而另一個有負值的機率就越高。這意味著在二進制形式中,很可能會有更多維度中一個是 0 而另一個是 1。這使它們在漢明距離上相距更遠。
相反的情況適用於距離較近的向量:非二進制向量越接近,在任何維度上都是 0 或都是 1 的機率就越高。這使它們在漢明距離上更接近。
Jina Embeddings 模型之所以特別適合二值化,是因為我們使用負面挖掘和其他微調實踐來訓練它們,特別是增加不相似事物之間的距離並減少相似事物之間的距離。這使得 embeddings 更穩健,對相似性和差異性更敏感,並使二進制 embeddings 之間的漢明距離與非二進制之間的餘弦距離更成比例。
tag使用 Jina AI 的 Binary Embeddings 可以節省多少?
採用 Jina AI 的 binary embedding 模型不僅可以降低時間敏感應用的延遲,還能帶來可觀的成本效益,如下表所示:
| 模型 | 每 2.5 億 embeddings 所需記憶體 |
檢索基準 平均 |
AWS 預估價格 (x2gb 實例 每 GB/月 $3.8) |
|---|---|---|---|
| 32-bit 浮點 embeddings | 715 GB | 47.13 | $35,021 |
| Binary embeddings | 22.3 GB | 42.05 | $1,095 |
僅有大約 10% 的檢索準確度下降,就能達到超過 95% 的儲存空間節省。
這比使用 OpenAI 的 Ada 2 模型或 Cohere 的 Embed v3所產生的二進制向量節省更多。這兩個模型產生的嵌入維度都在 1024 維以上。相較之下,Jina AI 的嵌入僅有 768 維,但效能仍然相當,這意味著在量化之前就已經比其他模型更小了,同時還保持著相同的準確度。
這些節省也具有環保意義,可以減少稀有材料的使用和能源消耗。
tag開始使用
要使用 Jina Embeddings API 獲取二進制嵌入,只需在 API 呼叫中添加 encoding_type 參數。使用值 binary 可以獲得以有符號整數編碼的二進制嵌入,或使用 ubinary 獲得無符號整數。
tag直接存取 Jina Embedding API
使用 curl:
curl https://api.jina.ai/v1/embeddings \
-H "Content-Type: application/json" \
-H "Authorization: Bearer <YOUR API KEY>" \
-d '{
"input": ["Your text string goes here", "You can send multiple texts"],
"model": "jina-embeddings-v2-base-en",
"encoding_type": "binary"
}'
或透過 Python requests API:
import requests
headers = {
"Content-Type": "application/json",
"Authorization": "Bearer <YOUR API KEY>"
}
data = {
"input": ["Your text string goes here", "You can send multiple texts"],
"model": "jina-embeddings-v2-base-en",
"encoding_type": "binary",
}
response = requests.post(
"https://api.jina.ai/v1/embeddings",
headers=headers,
json=data,
)
使用上述 Python request,透過檢查 response.json() 您將得到以下回應:
{
"model": "jina-embeddings-v2-base-en",
"object": "list",
"usage": {
"total_tokens": 14,
"prompt_tokens": 14
},
"data": [
{
"object": "embedding",
"index": 0,
"embedding": [
-0.14528547,
-1.0152762,
...
]
},
{
"object": "embedding",
"index": 1,
"embedding": [
-0.109809875,
-0.76077706,
...
]
}
]
}
這是兩個以 96 個 8 位元有符號整數儲存的二進制嵌入向量。要將它們解壓縮為 768 個 0 和 1,您需要使用 numpy 函式庫:
import numpy as np
# assign the first vector to embedding0
embedding0 = response.json()['data'][0]['embedding']
# convert embedding0 to a numpy array of unsigned 8-bit ints
uint8_embedding = np.array(embedding0).astype(numpy.uint8)
# unpack to binary
np.unpackbits(uint8_embedding)
結果是一個只包含 0 和 1 的 768 維向量:
array([0, 0, 1, 1, 0, 1, 1, 0, 1, 1, 0, 0, 0, 1, 0, 1, 1, 1, 1, 1, 0, 0,
0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 1, 1, 0, 0, 0, 1, 1, 1, 0, 1, 0, 1,
0, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 1, 1, 0, 0, 0, 0, 1, 0, 1, 1, 1,
0, 0, 0, 0, 1, 1, 1, 0, 0, 1, 0, 0, 0, 0, 1, 1, 1, 1, 0, 1, 0, 1,
1, 1, 0, 1, 1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 0, 0, 0,
0, 0, 1, 0, 0, 0, 1, 0, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1, 0, 0, 1, 0,
1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 1,
1, 0, 1, 0, 1, 1, 0, 0, 0, 1, 0, 1, 1, 1, 0, 0, 1, 1, 0, 0, 0, 1,
1, 1, 0, 1, 0, 1, 1, 1, 1, 0, 1, 0, 0, 1, 0, 0, 1, 0, 1, 0, 1, 1,
0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 1, 1, 0, 1, 0, 0, 0, 1, 1, 1,
1, 0, 0, 1, 0, 0, 0, 1, 0, 1, 0, 0, 1, 0, 1, 0, 1, 0, 0, 1, 0, 0,
0, 0, 0, 0, 1, 0, 0, 0, 1, 1, 1, 0, 1, 1, 0, 1, 1, 0, 1, 0, 0, 0,
1, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1, 1, 0, 1, 1, 0, 0, 0, 1, 0, 0, 1,
0, 0, 0, 0, 0, 1, 1, 0, 0, 1, 1, 1, 1, 0, 1, 0, 1, 0, 1, 1, 1, 1,
1, 0, 1, 0, 0, 0, 1, 0, 0, 1, 0, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 0,
0, 0, 0, 0, 1, 0, 1, 1, 1, 0, 1, 1, 1, 1, 0, 0, 0, 0, 0, 1, 1, 1,
1, 1, 1, 1, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 1, 0, 1, 0, 1,
1, 0, 1, 1, 1, 0, 0, 1, 0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 0, 0, 1, 1,
0, 0, 0, 1, 1, 1, 1, 1, 0, 1, 1, 0, 1, 0, 0, 0, 1, 1, 0, 1, 1, 0,
1, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 1, 1, 1, 0, 1, 1, 1, 0,
0, 0, 0, 0, 0, 1, 1, 1, 1, 0, 1, 0, 1, 1, 0, 1, 0, 1, 1, 1, 0, 0,
0, 0, 1, 1, 1, 0, 1, 0, 1, 0, 0, 1, 0, 1, 0, 0, 0, 1, 1, 1, 0, 1,
0, 1, 1, 1, 0, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 0, 0, 1, 0,
0, 1, 1, 1, 0, 1, 1, 0, 0, 1, 1, 0, 1, 1, 0, 1, 1, 1, 0, 1, 1, 0,
1, 1, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 1, 1, 1, 0, 1, 1, 0,
0, 1, 0, 0, 1, 1, 0, 1, 0, 0, 1, 0, 0, 1, 0, 1, 0, 1, 1, 1, 0, 0,
0, 0, 1, 1, 0, 1, 0, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 0, 1,
1, 0, 1, 1, 0, 1, 1, 0, 1, 0, 0, 1, 0, 0, 0, 1, 0, 1, 0, 1, 1, 0,
1, 1, 1, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1, 0, 0, 1, 0, 1, 1, 0, 0,
1, 0, 1, 1, 1, 1, 1, 1, 1, 0, 1, 0, 0, 0, 1, 0, 0, 1, 1, 1, 0, 1,
1, 1, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 1, 1, 0, 1, 1, 0, 0, 1, 1, 0,
1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 1, 0, 0, 1, 1, 0, 1,
1, 1, 1, 0, 0, 1, 1, 1, 0, 1, 0, 0, 1, 1, 0, 1, 1, 1, 1, 1, 1, 0,
1, 1, 1, 0, 0, 1, 1, 0, 0, 1, 0, 0, 1, 1, 0, 0, 0, 1, 0, 1, 1, 1,
0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 0, 1, 0, 0],
dtype=uint8)
tag在 Qdrant 中使用二進制量化
您也可以使用 Qdrant 的整合函式庫直接將二進制嵌入放入您的 Qdrant 向量存儲中。由於 Qdrant 內部已實作 BinaryQuantization,您可以將其作為整個向量集合的預設配置,這樣就可以在不改變程式碼的情況下檢索和儲存二進制向量。
請參見以下示例程式碼:
import qdrant_client
import requests
from qdrant_client.models import Distance, VectorParams, Batch, BinaryQuantization, BinaryQuantizationConfig
# 提供 Jina API 金鑰並選擇一個可用的模型。
# 您可以在此取得免費試用金鑰:https://jina.ai/embeddings/
JINA_API_KEY = "jina_xxx"
MODEL = "jina-embeddings-v2-base-en" # or "jina-embeddings-v2-base-en"
EMBEDDING_SIZE = 768 # 512 for small variant
# 從 API 獲取嵌入向量
url = "https://api.jina.ai/v1/embeddings"
headers = {
"Content-Type": "application/json",
"Authorization": f"Bearer {JINA_API_KEY}",
}
text_to_encode = ["Your text string goes here", "You can send multiple texts"]
data = {
"input": text_to_encode,
"model": MODEL,
}
response = requests.post(url, headers=headers, json=data)
embeddings = [d["embedding"] for d in response.json()["data"]]
# 將嵌入向量索引到 Qdrant
client = qdrant_client.QdrantClient(":memory:")
client.create_collection(
collection_name="MyCollection",
vectors_config=VectorParams(size=EMBEDDING_SIZE, distance=Distance.DOT, on_disk=True),
quantization_config=BinaryQuantization(binary=BinaryQuantizationConfig(always_ram=True)),
)
client.upload_collection(
collection_name="MyCollection",
ids=list(range(len(embeddings))),
vectors=embeddings,
payload=[
{"text": x} for x in text_to_encode
],
)要設定搜尋,您應該使用 oversampling 和 rescore 參數:
from qdrant_client.models import SearchParams, QuantizationSearchParams
results = client.search(
collection_name="MyCollection",
query_vector=embeddings[0],
search_params=SearchParams(
quantization=QuantizationSearchParams(
ignore=False,
rescore=True,
oversampling=2.0,
)
)
)tag使用 LlamaIndex
要在 LlamaIndex 中使用 Jina 二進位嵌入向量,在實例化 JinaEmbedding 物件時將 encoding_queries 參數設定為 binary:
from llama_index.embeddings.jinaai import JinaEmbedding
# 您可以從 https://jina.ai/embeddings/ 獲取免費試用金鑰
JINA_API_KEY = "<YOUR API KEY>"
jina_embedding_model = JinaEmbedding(
api_key=jina_ai_api_key,
model="jina-embeddings-v2-base-en",
encoding_queries='binary',
encoding_documents='float'
)
jina_embedding_model.get_query_embedding('Query text here')
jina_embedding_model.get_text_embedding_batch(['X', 'Y', 'Z'])
tag支援二進位嵌入向量的其他向量資料庫
以下向量資料庫提供二進位向量的原生支援:
tag範例
為了展示二進位嵌入向量的效果,我們從 arXiv.org 選取了一些摘要,並使用 jina-embeddings-v2-base-en 獲取了它們的 32 位元浮點數和二進位向量。然後我們將它們與示例查詢「3D segmentation」的嵌入向量進行比較。
從下表可以看出,前三個答案是相同的,前五個中有四個匹配。使用二進位向量產生了幾乎相同的最佳匹配結果。
| Binary | 32-bit Float | |||
|---|---|---|---|---|
| 排名 | 漢明 距離 |
匹配文本 | 餘弦值 | 匹配文本 |
| 1 | 0.1862 | SEGMENT3D: A Web-based Application for Collaboration... |
0.2340 | SEGMENT3D: A Web-based Application for Collaboration... |
| 2 | 0.2148 | Segmentation-by-Detection: A Cascade Network for... |
0.2857 | Segmentation-by-Detection: A Cascade Network for... |
| 3 | 0.2174 | Vox2Vox: 3D-GAN for Brain Tumour Segmentation... |
0.2973 | Vox2Vox: 3D-GAN for Brain Tumour Segmentation... |
| 4 | 0.2318 | DiNTS: Differentiable Neural Network Topology Search... |
0.2983 | Anisotropic Mesh Adaptation for Image Segmentation... |
| 5 | 0.2331 | Data-Driven Segmentation of Post-mortem Iris Image... |
0.3019 | DiNTS: Differentiable Neural Network Topology... |