子空間餘弦相似度是否意味著高維度餘弦相似度？

💡

2024 年 1 月 25 日，OpenAI 發布了一個新的 embedding 模型，其中包含一個名為「shortening」的新功能，該功能允許開發者在不影響 embedding 有效表達概念能力的前提下，從序列末尾裁剪數值。本文將深入探討這項創新背後的理論基礎和合理性。

思考這個問題：當在高維空間中測量 embedding 向量的餘弦相似度時，它們在低維子空間的相似度如何影響整體相似度？這是一個直接的比例關係，還是高維資料的情況更為複雜？

更具體地說，向量在前 256 維的高度相似是否能確保它們在完整的 768 維中也具有高度相似性？相反地，如果向量在某些維度上有顯著差異，是否意味著整體相似度較低？這些不僅僅是理論思考，它們對向量檢索、資料庫索引和 RAG 系統的效能都至關重要。

開發者經常依賴經驗法則，假設子空間的高相似度等同於整體的高相似度，或者某一維度的顯著差異會大幅影響整體相似度。問題是：這些啟發式方法是建立在堅實的理論基礎上，還是僅僅是為了方便而做出的假設？

本文將深入探討這些問題，研究子空間相似度與整體向量相似度之間的理論關係及其實際應用。

tag餘弦相似度的界限

給定向量 $\mathbf{A}, \mathbf{B}\in \mathbb{R}^d$ ，我們將它們分解為 $\mathbf{A}=[\mathbf{A}_1, \mathbf{A}_2]$ 和 $\mathbf{B}=[\mathbf{B}_1, \mathbf{B}_2]$ ，其中 $\mathbf{A}_1,\mathbf{B}_1\in\mathbb{R}^m$ 且 $\mathbf{A}_2,\mathbf{B}_2\in\mathbb{R}^n$ ，且 $m+n=d$ 。

在子空間 $\mathbb{R}^m$ 中的餘弦相似度為 $\cos(\mathbf{A}_1, \mathbf{B}_1)=\frac{\mathbf{A}_1\cdot\mathbf{B}_1}{\|\mathbf{A}_1\|\|\mathbf{B}_1\|}$ ；同樣地，在子空間 $\mathbb{R}^n$ 中的相似度為 $\cos(\mathbf{A}_2, \mathbf{B}_2)=\frac{\mathbf{A}_2\cdot\mathbf{B}_2}{\|\mathbf{A}_2\|\|\mathbf{B}_2\|}$ 。

在原始空間 $\mathbb{R}^d$ 中，餘弦相似度定義為： $\begin{align*}\cos(\mathbf{A},\mathbf{B})&=\frac{\mathbf{A}\cdot\mathbf{B}}{\|\mathbf{A}\|\|\mathbf{B}\|}\\&=\frac{\mathbf{A}_1\cdot\mathbf{B}_1+\mathbf{A}_2\cdot\mathbf{B}_2}{\sqrt{\|\mathbf{A}_1\|^2+\|\mathbf{A}_2\|^2}\sqrt{\|\mathbf{B}_1\|^2+\|\mathbf{B}_2\|^2}}\\&=\frac{\cos(\mathbf{A}_1, \mathbf{B}_1)\|\mathbf{A}_1\|\|\mathbf{B}_1\|+\cos(\mathbf{A}_2, \mathbf{B}_2)\|\mathbf{A}_2\|\|\mathbf{B}_2\|}{\sqrt{\|\mathbf{A}_1\|^2+\|\mathbf{A}_2\|^2}\sqrt{\|\mathbf{B}_1\|^2+\|\mathbf{B}_2\|^2}}\end{align*}$

現在，令 $s := \max(\cos(\mathbf{A}_1, \mathbf{B}_1), \cos(\mathbf{A}_2, \mathbf{B}_2))$ 。則我們有： $\begin{align*}\cos(\mathbf{A},\mathbf{B})&\leq\frac{s\|\mathbf{A}_1\|\|\mathbf{B}_1\|+s\|\mathbf{A}_2\|\|\mathbf{B}_2\|}{\sqrt{\|\mathbf{A}_1\|^2+\|\mathbf{A}_2\|^2}\sqrt{\|\mathbf{B}_1\|^2+\|\mathbf{B}_2\|^2}}\\&=\frac{\|\mathbf{A}_1\|\|\mathbf{B}_1\|+\|\mathbf{A}_2\|\|\mathbf{B}_2\|}{\sqrt{\|\mathbf{A}_1\|^2+\|\mathbf{A}_2\|^2}\sqrt{\|\mathbf{B}_1\|^2+\|\mathbf{B}_2\|^2}}\cdot s\\&=\cos(\underbrace{[\|\mathbf{A}_1\|, \|\mathbf{A}_2\|]}_{\mathbb{R}^2}, \underbrace{[\|\mathbf{B}_1\|, \|\mathbf{B}_2\|]}_{\mathbb{R}^2})\cdot s\\&\leq 1\cdot s \\&= \max(\cos(\mathbf{A}_1, \mathbf{B}_1), \cos(\mathbf{A}_2, \mathbf{B}_2))\end{align*}$

證明完畢。

注意，在證明的最後一步中，我們利用了餘弦相似度總是小於等於 1 的特性。這構成了我們的上界。同樣地，我們可以證明 $\cos(\mathbf{A},\mathbf{B})$ 的下界為：

$\cos(\mathbf{A},\mathbf{B}) \geq t \cdot \cos([\|\mathbf{A}_1\|, \|\mathbf{A}_2\|], [\|\mathbf{B}_1\|, \|\mathbf{B}_2\|])$ ，其中 $t:= \min(\cos(\mathbf{A}_1, \mathbf{B}_1), \cos(\mathbf{A}_2, \mathbf{B}_2))$ 。

注意，對於下界，我們不能急於得出 $\cos(\mathbf{A},\mathbf{B}) \geq t$ 的結論。這是因為餘弦函數的範圍在 $[-1, 1]$ 之間。由於這個範圍，我們無法建立比平凡值 -1 更緊的下界。

因此總結來說，我們有以下寬鬆的界限： $-1\leq\cos(\mathbf{A},\mathbf{B})\leq\max(\cos(\mathbf{A}_1, \mathbf{B}_1), \cos(\mathbf{A}_2, \mathbf{B}_2)).$ 和一個更緊的界限 $\begin{align*} \gamma \cdot t\leq&\cos(\mathbf{A}, \mathbf{B}) \leq\gamma\cdot s\\\gamma \cdot \min(\cos(\mathbf{A}_1, \mathbf{B}_1), \cos(\mathbf{A}_2, \mathbf{B}_2)) \leq &\cos(\mathbf{A}, \mathbf{B}) \leq \gamma \cdot \max(\cos(\mathbf{A}_1, \mathbf{B}_1), \cos(\mathbf{A}_2, \mathbf{B}_2))\end{align*}$ ，其中 $\gamma = \cos([\|\mathbf{A}_1\|, \|\mathbf{A}_2\|], [\|\mathbf{B}_1\|, \|\mathbf{B}_2\|])$ 。

tag與 Johnson–Lindenstrauss 引理的關聯

JL 引理指出，對於任意 $0 < \epsilon < 1$ 和任意有限點集 $S$ 在 $\mathbb{R}^d$ 中，存在一個映射 $f: \mathbb{R}^d \rightarrow \mathbb{R}^k$ （其中 $k = O(\epsilon^{-2} \log |S|)$ ）使得對於所有 $\mathbf{u}, \mathbf{v} \in S$ ，歐式距離大致得以保留：

$(1 - \epsilon) \|\mathbf{u} - \mathbf{v}\|^2 \leq \|f(\mathbf{u}) - f(\mathbf{v})\|^2 \leq (1 + \epsilon) \|\mathbf{u} - \mathbf{v}\|^2$

為了使 $f$ 像子空間選擇一樣工作，我們可以使用對角矩陣進行投影，例如一個 $5 \times 3$ 矩陣 $f$ ，儘管不是隨機的（注意，JL 引理的典型表述涉及通常使用從高斯分布中抽取的隨機矩陣的線性變換）。例如，如果我們想要從五維向量空間中保留第 1、3 和第 5 維，矩陣 $f$ 可以設計如下： $f = \begin{bmatrix}1 & 0 & 0 \\0 & 0 & 0 \\0 & 1 & 0 \\0 & 0 & 0 \\0 & 0 & 1\end{bmatrix}$
然而，通過將 $f$ 限定為對角矩陣，我們限制了可用於投影的函數類別。JL 引理保證了在更廣泛的線性變換類別中存在合適的 $f$ ，但當我們將 $f$ 限制為對角矩陣時，在這個受限的類別中可能不存在適合應用 JL 引理界限的 $f$ 。

tag驗證界限

為了經驗性地探索高維向量空間中餘弦相似度的理論界限，我們可以使用蒙特卡羅模擬。這種方法允許我們生成大量隨機向量對，計算它們在原始空間和子空間中的相似度，然後評估理論上界和下界在實踐中的適用性。

以下 Python 程式碼片段實現了這個概念。它隨機生成高維空間中的向量對並計算它們的餘弦相似度。然後，它將每個向量分為兩個子空間，計算每個子空間內的餘弦相似度，並根據子空間相似度評估全維度餘弦相似度的上界和下界。

import numpy as np


def compute_cosine_similarity(U, V):
    # Normalize the rows to unit vectors
    U_norm = U / np.linalg.norm(U, axis=1, keepdims=True)
    V_norm = V / np.linalg.norm(V, axis=1, keepdims=True)
    # Compute pairwise cosine similarity
    return np.sum(U_norm * V_norm, axis=1)


# Generate random data
num_points = 5000
d = 1024
A = np.random.random([num_points, d])
B = np.random.random([num_points, d])

# Compute cosine similarity between A and B
cos_sim = compute_cosine_similarity(A, B)

# randomly divide A and B into subspaces
m = np.random.randint(1, d)
A1 = A[:, :m]
A2 = A[:, m:]
B1 = B[:, :m]
B2 = B[:, m:]

# Compute cosine similarity in subspaces
cos_sim1 = compute_cosine_similarity(A1, B1)
cos_sim2 = compute_cosine_similarity(A2, B2)

# Find the element-wise maximum and minimum of cos_sim1 and cos_sim2
s = np.maximum(cos_sim1, cos_sim2)
t = np.minimum(cos_sim1, cos_sim2)

norm_A1 = np.linalg.norm(A1, axis=1)
norm_A2 = np.linalg.norm(A2, axis=1)
norm_B1 = np.linalg.norm(B1, axis=1)
norm_B2 = np.linalg.norm(B2, axis=1)

# Form new vectors in R^2 from the norms
norm_A_vectors = np.stack((norm_A1, norm_A2), axis=1)
norm_B_vectors = np.stack((norm_B1, norm_B2), axis=1)

# Compute cosine similarity in R^2
gamma = compute_cosine_similarity(norm_A_vectors, norm_B_vectors)

# print some info and validate the lower bound and upper bound
print('d: %d\n'
      'm: %d\n'
      'n: %d\n'
      'avg. cosine(A,B): %f\n'
      'avg. upper bound: %f\n'
      'avg. lower bound: %f\n'
      'lower bound satisfied: %s\n'
      'upper bound satisfied: %s' % (
          d, m, (d - m), np.mean(cos_sim), np.mean(s), np.mean(gamma * t), np.all(s >= cos_sim),
          np.all(gamma * t <= cos_sim)))

用於驗證餘弦相似度邊界的蒙特卡洛驗證器

d: 1024
m: 743
n: 281
avg. cosine(A,B): 0.750096
avg. upper bound: 0.759080
avg. lower bound: 0.741200
lower bound satisfied: True
upper bound satisfied: True

我們的蒙特卡洛驗證器的範例輸出。需要注意的是，lower/upper bound satisfied條件是針對每個向量單獨檢查的。同時，avg. lower/upper bound提供了與這些邊界相關的統計概覽，但並不直接影響驗證過程。

tag理解邊界

簡而言之，當比較兩個高維向量時，整體相似度介於其子空間最佳和最差相似度之間，並根據這些子空間在整體方案中的大小或重要性進行調整。這就是高維空間中餘弦相似度邊界所直觀表示的：根據各部分的相對大小或重要性，在最相似和最不相似部分之間取得平衡。

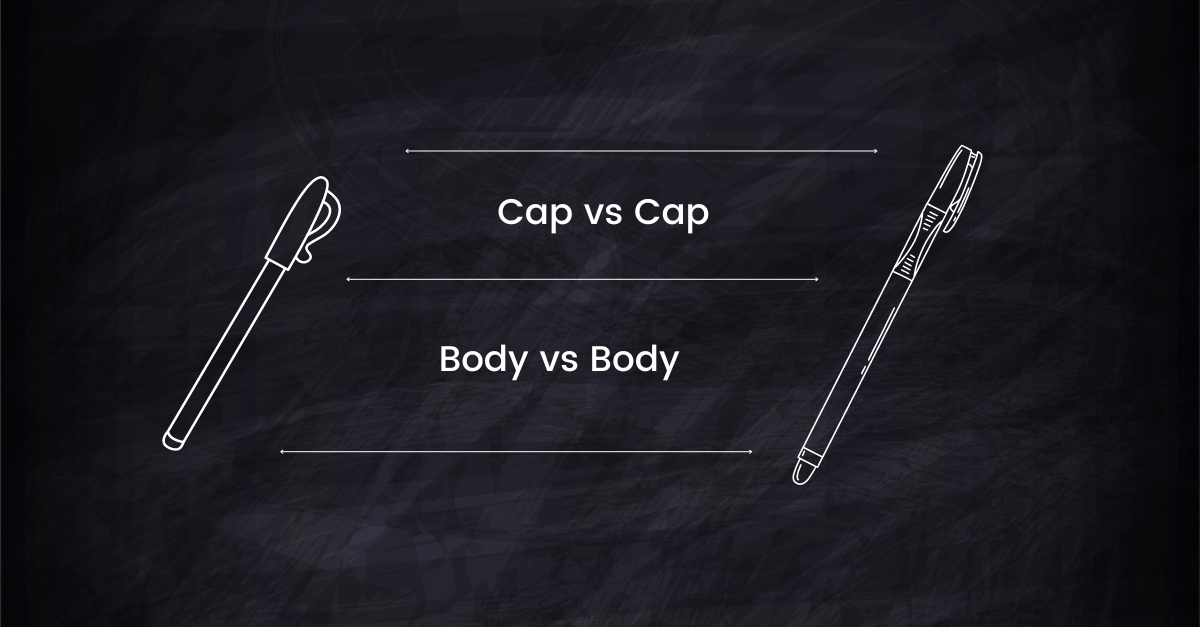
在黑色背景上帶有標籤部分的兩支觸控筆筆帽和筆身的比較圖 — 每支筆都有兩個主要組件：筆身和筆帽。

想像你正試圖比較兩個多部件物體（比如說，兩支精美的筆）的整體相似度。每支筆都有兩個主要組件：筆身和筆帽。我們要確定的是整支筆（包括筆身和筆帽）的相似度：

tag上界 ( $\gamma \cdot s$ )

將 $s$ 理解為筆的對應部件之間的最佳匹配。如果筆帽很相似但筆身不相似， $s$ 就是筆帽的相似度。

而 $\gamma$ 則是基於每個部分的大小（或重要性）的縮放因子。如果一支筆有很長的筆身和短的筆帽，而另一支筆有短的筆身和長的筆帽， $\gamma$ 就會根據這些比例差異調整整體相似度。

上界告訴我們，無論某些部分多麼相似，整體相似度都不能超過這個經過比例因子縮放的"最佳部分相似度"。

tag下界 ( $\gamma \cdot t$ )

這裡， $t$ 是最不匹配部分的相似度。如果筆身差異很大但筆帽相似， $t$ 就反映了筆身的相似度。

同樣， $\gamma$ 根據每個部分的比例進行縮放。

下界意味著考慮每個部分的比例後，整體相似度不會比這個"最差部分相似度"更差。

tag邊界的含義

對於使用嵌入、向量搜索、檢索或資料庫的軟體工程師來說，理解這些邊界具有實際意義，特別是在處理高維數據時。向量搜索通常涉及在資料庫中找到與給定查詢向量最接近（最相似）的向量，通常使用餘弦相似度作為接近度的度量。我們討論的邊界可以為此類任務使用子空間相似度的有效性和限制提供見解。

tag使用子空間相似度進行排序

安全性和準確性：使用子空間相似度進行排序和檢索 top-k 結果可能是有效的，但需要謹慎。上界表明整體相似度不能超過子空間的最大相似度。因此，如果一對向量在特定子空間中高度相似，它很可能在高維空間中也相似。

潛在陷阱：然而，下界表明在一個子空間中相似度低的兩個向量在整體上仍可能相當相似。因此，單純依賴子空間相似度可能會遺漏一些相關結果。

tag誤解和注意事項

過度估計子空間重要性：一個常見的誤解是過度估計特定子空間的重要性。雖然在一個子空間中的高相似度是個好的指標，但由於其他子空間的影響，它並不能保證整體相似度高。

忽略負相似度：在子空間中餘弦相似度為負的情況下，表示在該維度上存在對立關係。工程師應該注意這些負相似度如何影響整體相似度。