Умеют ли модели Embedding/Reranker сравнивать числа?

На такой вопрос меня спросили сегодня на конференции ICML в Вене.

Во время кофе-брейка ко мне подошел пользователь Jina с вопросом, возникшим из недавних обсуждений в сообществе LLM. Он спросил, может ли наша модель для создания эмбеддингов определить, что 9.11 меньше, чем 9.9 - задача, в которой многие LLM дают противоположный ответ.

«Честно говоря, я не знаю», - ответил я. Когда он объяснил важность этой возможности для его приложения и предположил, что токенизация может быть корнем проблемы, я кивнул в знак согласия - мой разум уже генерировал идеи для эксперимента, чтобы найти ответ.

В этой статье я хочу проверить, могут ли наша модель эмбеддингов jina-embeddings-v2-base-en (выпущенная в октябре 2023) и Reranker jina-reranker-v2-multilingual (выпущенный в июне 2024) точно сравнивать числа. Чтобы расширить область исследования за пределы простого сравнения 9.11 и 9.9, я разработал набор экспериментов, включающих различные типы чисел: малые целые числа, большие числа, числа с плавающей точкой, отрицательные числа, валюту, даты и время. Цель состоит в том, чтобы оценить эффективность наших моделей в обработке различных числовых форматов.

tagЭкспериментальная установка

Полную реализацию можно найти в Colab ниже:

Дизайн эксперимента довольно прост. Например, чтобы проверить, понимает ли модель эмбеддингов числа между [1, 100]. Шаги следующие:

Создание документов: Генерируем «строковые литералы» документов для каждого числа от 1 до 100.
Отправка в API эмбеддингов: Используем API эмбеддингов для получения эмбеддингов для каждого документа.
Вычисление косинусного сходства: Вычисляем попарное косинусное сходство для каждых двух документов, создавая матрицу сходства.
Создание диаграммы рассеяния: Визуализируем результаты с помощью диаграммы рассеяния. Каждый элемент $(i, j)$ в матрице сходства отображается как точка с: Ось X: $(i - j)$ ; Ось Y: значение сходства $(i, j)$

Если дельта $(i - j)$ равна нулю, т.е. $i = j$ , то семантическое сходство должно быть наивысшим. По мере увеличения дельты $(i - j)$ сходство должно уменьшаться. В идеале, сходство должно быть линейно пропорционально значению дельты. Если мы не наблюдаем такой линейности, то вероятно, что модель не может понимать числа и может выдавать ошибки, например, что 9.11 больше, чем 9.9.

Модель Reranker следует аналогичной процедуре. Ключевое отличие в том, что мы перебираем созданные документы, устанавливая каждый как query, добавляя в начало промпт "what is the closest item to..." и ранжируя все остальные как documents. Оценка релевантности, возвращаемая API Reranker, используется непосредственно как мера семантического сходства. Основная реализация выглядит следующим образом.

def rerank_documents(documents):
    reranker_url = "https://api.jina.ai/v1/rerank"
    headers = {
        "Content-Type": "application/json",
        "Authorization": f"Bearer {token}"
    }

    # Initialize similarity matrix
    similarity_matrix = np.zeros((len(documents), len(documents)))

    for idx, d in enumerate(documents):
        payload = {
            "model": "jina-reranker-v2-base-multilingual",
            "query": f"what is the closest item to {d}?",
            "top_n": len(documents),
            "documents": documents
        }
    ...

tagМогут ли модели сравнивать числа между [1, 2, 3, ..., 100]?

Диаграмма рассеяния со средним значением и дисперсией для каждой дельты. Слева: jina-embeddings-v2-base-en; Справа: jina-reranker-v2-multilingual. documents = [str(i) for i in range(1, 101)]

tagКак читать эти графики

Прежде чем перейти к следующим экспериментам, позвольте мне сначала объяснить, как правильно читать эти графики. Во-первых, мое наблюдение из двух графиков выше показывает, что модель эмбеддингов работает хорошо, тогда как модель ранжирования справляется не так хорошо. Так что же мы видим и почему?

Ось X представляет дельту индексов $(i,j)$ , или $i-j$ , когда мы равномерно выбираем $d_i$ и $d_j$ из наших наборов документов. Эта дельта варьируется от $[-100, 100]$ . Поскольку наш набор документов отсортирован по построению, т.е. чем меньше $|i-j|$ , тем ближе $d_i$ и $d_j$ семантически; чем дальше друг от друга $i$ и $j$ , тем ниже сходство между $d_i$ и $d_j$ . Вот почему вы видите пик сходства (представленного осью Y) при $X=0$ , который затем линейно падает при движении влево и вправо.

В идеале это должно создавать острый пик или форму "стрелки вверх" как ^. Однако это не всегда так. Если зафиксировать ось X в точке, скажем $X=25$ , и посмотреть вдоль оси Y, вы найдете значения сходства от 0.80 до 0.95. Это означает, что $\mathrm{sim}(d_27, d_2)$ может быть 0.81, тогда как $\mathrm{sim}(d_42, d_17)$ может быть 0.91, несмотря на то, что их дельта равна 25.

Голубая линия тренда показывает среднее сходство для каждого значения X со стандартным отклонением. Также обратите внимание, что сходство должно падать линейно, поскольку наш набор документов равномерно распределен, обеспечивая равные интервалы между смежными документами.

Заметьте, что графики эмбеддингов будут всегда симметричными, с максимальным значением Y равным 1.0 при $X=0$ . Это потому, что косинусное сходство симметрично для $d_i$ и $d_j$ , и $\cos(0)=1$ .

С другой стороны, графики ранжирования всегда асимметричны из-за различных ролей запроса и документов в модели ранжирования. Максимальное значение вероятно не будет равно 1.0, потому что $X=0$ означает, что мы используем ранжировщик для вычисления оценки релевантности "what is the closest item to 4" vs "4". Если подумать об этом, нет гарантии, что $X=0$ приведет к максимальному значению Y.

tagМогут ли модели сравнивать отрицательные числа между [-100, -99, -98, ..., -1]?

Диаграмма рассеяния со средним значением и дисперсией для каждой дельты. Слева: jina-embeddings-v2-base-en; Справа: jina-reranker-v2-multilingual. Здесь мы хотим проверить, может ли модель определять семантическое сходство в отрицательном пространстве. documents = [str(-i) for i in range(1, 101)]

tagМогут ли модели сравнивать числа с большими интервалами [1000, 2000, 3000, ..., 100000]?

Здесь мы хотим проверить, может ли модель определять семантическое сходство при сравнении чисел с интервалом 1000. documents = [str(i*1000) for i in range(1, 101)] График рассеяния со средним значением и дисперсией для каждой дельты. Слева: jina-embeddings-v2-base-en; Справа: jina-reranker-v2-multilingual.

tagМогут ли модели сравнивать числа из произвольного диапазона, например [376, 377, 378, ..., 476]?

Здесь мы хотим проверить, может ли модель определять семантическое сходство при сравнении чисел в произвольном диапазоне, поэтому мы переместили числа в случайный диапазон documents = [str(i+375) for i in range(1, 101)] . График рассеяния со средним значением и дисперсией для каждой дельты. Слева: jina-embeddings-v2-base-en; Справа: jina-reranker-v2-multilingual.

tagМогут ли модели сравнивать большие числа в диапазоне [4294967296, 4294967297, 4294967298, ..., 4294967396]?

Здесь мы хотим проверить, может ли модель определять семантическое сходство при сравнении очень больших чисел. Аналогично идее предыдущего эксперимента, мы переместили диапазон дальше к большому числу. documents = [str(i+4294967296) for i in range(1, 101)] График рассеяния со средним значением и дисперсией для каждой дельты. Слева: jina-embeddings-v2-base-en; Справа: jina-reranker-v2-multilingual.

tagМогут ли модели сравнивать дробные числа в диапазоне [0.0001, 0.0002, 0.0003, ..., 0.1]? (без фиксированного количества знаков после запятой)

Здесь мы хотим проверить, может ли модель определять семантическое сходство при сравнении дробных чисел. documents = [str(i/1000) for i in range(1, 101)] График рассеяния со средним значением и дисперсией для каждой дельты. Слева: jina-embeddings-v2-base-en; Справа: jina-reranker-v2-multilingual.

tagМогут ли модели сравнивать денежные величины в диапазоне [ $1,$ 2, $3, ...,$ 100]?

Здесь мы хотим проверить, может ли модель определять семантическое сходство при сравнении чисел в денежном формате. documents = ['$'+str(i) for i in range(1, 101)] График рассеяния со средним значением и дисперсией для каждой дельты. Слева: jina-embeddings-v2-base-en; Справа: jina-reranker-v2-multilingual.

tagМогут ли модели сравнивать даты в диапазоне [2024-07-24, 2024-07-25, 2024-07-26, ..., 2024-10-31]?

Здесь мы хотим проверить, может ли модель определять семантическое сходство при сравнении чисел в формате даты, т.е. ГГГГ-ММ-ДД. today = datetime.today(); documents = [(today + timedelta(days=i)).strftime('%Y-%m-%d') for i in range(100)] График рассеяния со средним значением и дисперсией для каждой дельты. Слева: jina-embeddings-v2-base-en; Справа: jina-reranker-v2-multilingual.

tagМогут ли модели сравнивать время в диапазоне [19:00:07, 19:00:08, 19:00:09,..., 20:39:07]?

Здесь мы хотим проверить, может ли модель определять семантическое сходство при сравнении чисел во временном формате, т.е. hh:mm:ss. now = datetime.now(); documents = [(now + timedelta(minutes=i)).strftime('%H:%M:%S') for i in range(100)]. График рассеяния со средним значением и дисперсией для каждой дельты. Слева: jina-embeddings-v2-base-en; Справа: jina-reranker-v2-multilingual.

tagНаблюдения

Вот некоторые наблюдения из приведенных выше графиков:

tagМодели ранжирования

Модели ранжирования испытывают трудности при сравнении чисел. Даже в простейшем случае сравнения чисел в диапазоне [1, 100] их производительность неудовлетворительна.
Важно отметить особую конструкцию промпта, используемую для запросов в нашем ранжировании, т.е. what is the closest item to x, так как это также может влиять на результаты.

tagМодели эмбеддингов

Модели эмбеддингов показывают достаточно хорошие результаты при сравнении небольших целых чисел в диапазоне [1, 100] или отрицательных чисел в диапазоне [-100, 1]. Однако их производительность значительно снижается при смещении этого диапазона к другим значениям, добавлении большего количества интервалов или работе с большими или меньшими числами с плавающей запятой.
Регулярные выбросы наблюдаются через определенные интервалы, обычно каждые 10 шагов. Это поведение может быть связано с тем, как токенизатор обрабатывает строки, потенциально разбивая строку на "10" или "1" и "0".

tagПонимание даты и времени

Интересно, что модели эмбеддингов, похоже, хорошо понимают даты и время, правильно сравнивая их в большинстве случаев. Для графиков дат выбросы появляются каждые 30/31 шагов, что соответствует количеству дней в месяце. Для графиков времени выбросы появляются каждые 60 шагов, что соответствует минутам в часе.
Модели ранжирования также, похоже, до некоторой степени улавливают это понимание.

tagВизуализация сходства с "нулем"

Обновлено 29 июля 2024

Другой интересный эксперимент, который, вероятно, более интуитивен, заключается в прямой визуализации оценки сходства или релевантности между любым числом и нулем (т.е. началом координат). Зафиксировав точку отсчета как эмбеддинг нуля, мы хотим увидеть, уменьшается ли семантическое сходство линейно по мере увеличения чисел. Для ранжировщика мы можем зафиксировать запрос как "0" или "What is the closest number to number zero?" и ранжировать все числа, чтобы увидеть, уменьшаются ли их оценки релевантности по мере увеличения чисел. Результаты показаны ниже:

Здесь мы фиксируем "начальный эмбеддинг" как эмбеддинг "нуля" и проверяем, пропорционально ли семантическое сходство между любым числом и нулем значению числа. В частности, мы используем documents = [str(i) for i in range(2048)]. Показан график рассеяния со средним значением и дисперсией для каждой дельты. Слева: jina-embeddings-v2-base-en; Справа: jina-reranker-v2-multilingual.

tagЗаключение

Эта статья иллюстрирует, как наши текущие модели эмбеддингов и ранжирования обрабатывают сравнение чисел. Несмотря на относительно простую экспериментальную настройку, она выявляет некоторые фундаментальные недостатки в текущих моделях и предоставляет ценную информацию для разработки наших следующих версий эмбеддингов и ранжировщика.

Два ключевых фактора определяют, может ли модель точно сравнивать числа:

Во-первых, токенизация: Если словарь включает только цифры 0-9, тогда 11 может быть токенизировано как отдельные токены 1 и 1, или как единый токен 11. Этот выбор влияет на понимание числовых значений моделью.

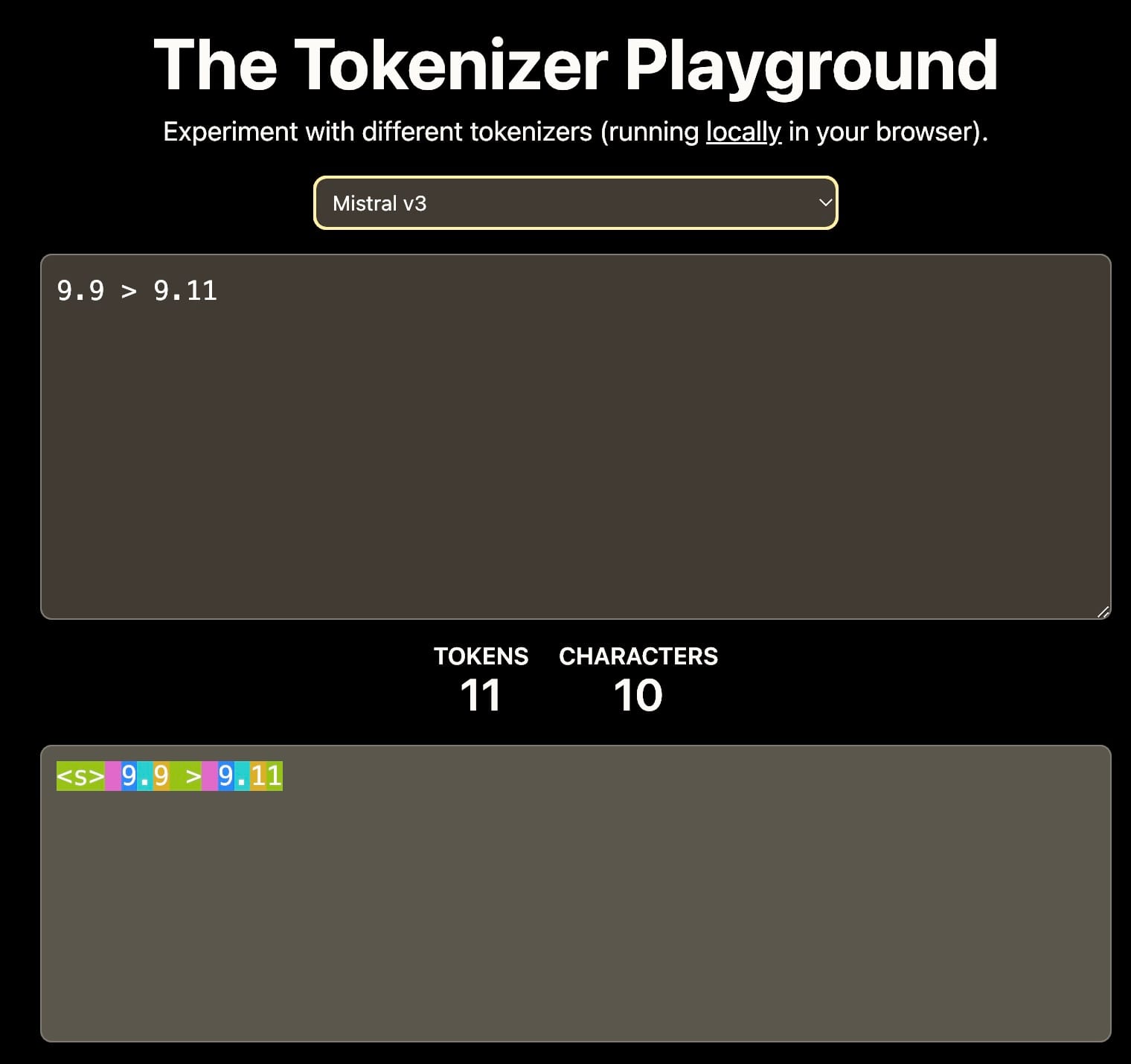
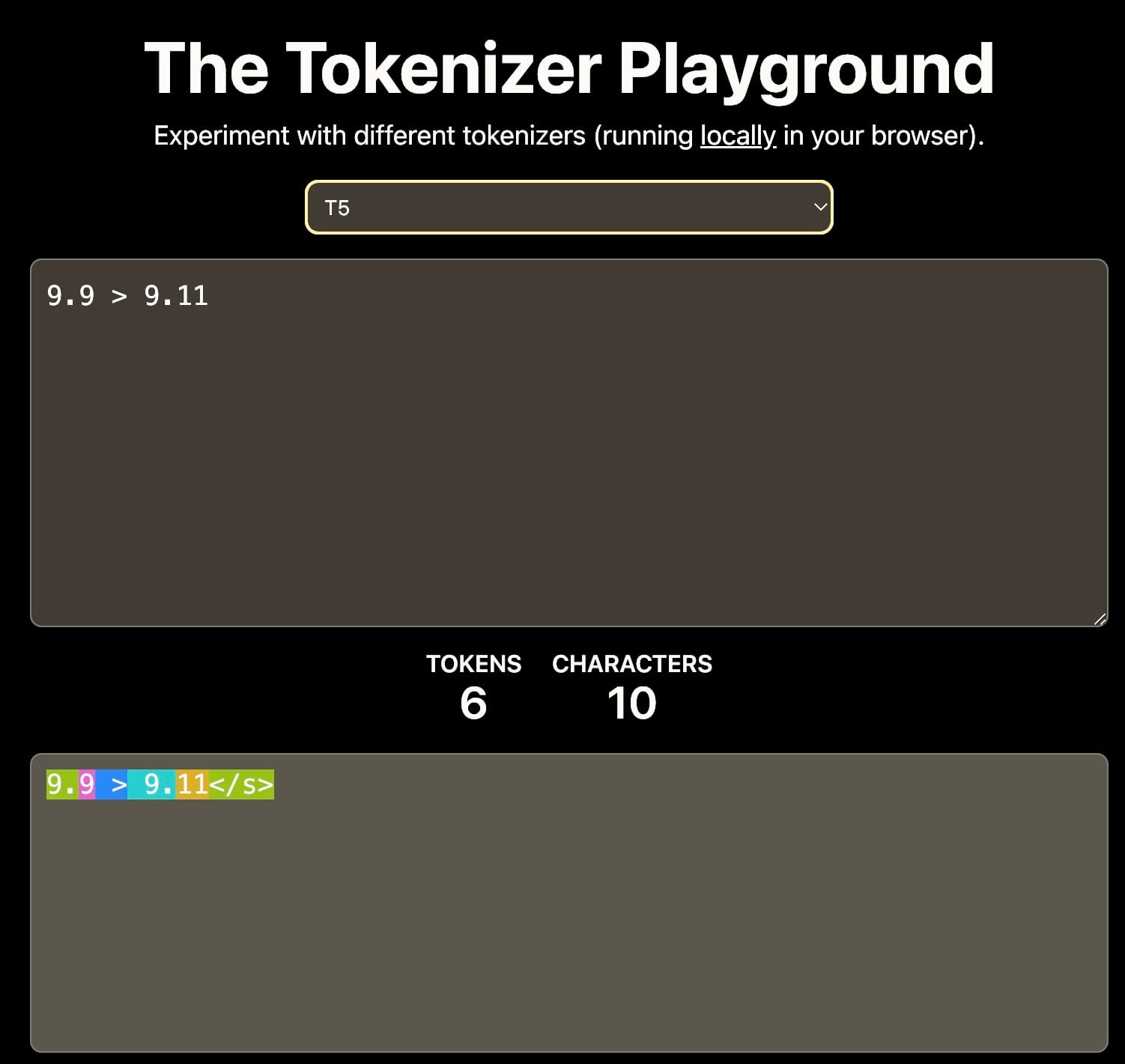
Разные токенизаторы приводят к разной интерпретации 9.11. Это может влиять на последующее контекстное обучение. Источник: The Tokenizer Playground на HuggingFace.

Во-вторых, обучающие данные: Обучающий корпус значительно влияет на способности модели к числовым рассуждениям. Например, если обучающие данные в основном включают программную документацию или репозитории GitHub, где распространена семантическая версионность, модель может интерпретировать, что 9.11 больше, чем 9.9, поскольку 9.11 является минорной версией, следующей за 9.9.

Арифметические возможности моделей плотного поиска, таких как эмбеддинги и ранжировщики, крайне важны для задач, включающих RAG и продвинутый поиск и рассуждения. Сильные способности к числовым рассуждениям могут значительно улучшить качество поиска, особенно при работе со структурированными данными, такими как JSON.